Advanced Machine Learning 2 | Basics of PyTorch and Backpropagation

1. Basics For PyTorch

(1) History of PyTorch

PyTorch began as an internship project by Adam Paszke, which is a part of the Torch library. Torch is an open-source machine learning library, a scientific computing framework, and a script language based on the Lua programming language. It had an initial release October 2002.

(2) Features of PyTorch

• Big codebase on CPU and GPU
• Large team of professional developers
• Used in thousands of academic papers
• Deployed by Facebook, Uber, Tesla, Microsoft, OpenAI, etc.

2. Mathematics Behind PyTorch

(1) Central Difference

Generally, we have two ways for calculating derivatives. In the previous sections (i.e. Introduction to machine learning) we have talked about, we have used a symbolic derivatives which means that we need full symbolic function. Even though this method is accurate, we can hardly calculate the derivatives when the symbolic function is unclear. Therefore, the second approach we have here is called the numerical derivatives.

Althought this formula will not give us an accurate value of derivative, it provides flexibility. Here, we can have an example function where we select $\epsilon = 0.0001$, which can be modified case by case.

1
def central_difference(func, x):
2
    eps = 0.0001
3
    return (func(x + eps) - func(x - eps)) / (2 * eps)

(2) Autodifferentiation

Automatic differentiation (aka. AD or autodiff) a set of techniques to evaluate the derivative of a function specified by a computer program based on the chain rule. There are two different kinds of pass strategy,

• Forward pass: means to compute the arbitrary function
• Backward pass: means to compute the derivatives of the function

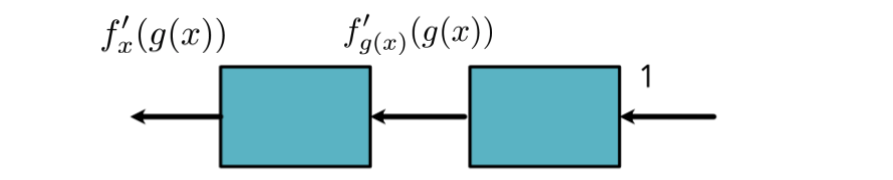
Suppose now we would like to run backward pass on one function $f(x) = x^2$, and we have already known that it has derivative $f'(x) = 2x$. Then we can write it in code as,

xxxxxxxxxx
11
1
class square:
2
    
3
    def __init__(self, x):
4
        self.x = x
5
        return
6
    
7
    def forward(self):
8
        return self.x**2
9
    
10
    def backward(self, d_out):
11
        return 2 * self.x * d_out

Note that if we want to calculate the backward pass of $x = 1$ in this one function situation, we should pass d_out = 1 as square(1).backward(1) .

Now let's consider the two-function backward with one argument. So here is a forward pass of function $g$ and $f$ on $x$ that shows as follows,

​x
1
# pseudo code
2
class f:
3
  def forward(self, x):
4
    self.x = x
5
    return f(x)
6
​
7
class g:
8
  def forward(self, x):
9
    self.x = x
10
    return g(x)
11
  
12
result = f.forward(g.forward(x))

If we use the univariate chain rule, we can have,

Which means we can extend the former class definitions by,

xxxxxxxxxx
22
1
# pseudo code
2
class f:
3
  def forward(self, x):
4
    self.x = x
5
    return f(x)
6
  
7
  def backward(self, d_out):
8
    return df(self.x) * d_out
9
  
10
  def df(self):
11
    return central_difference(f, self.x)
12
​
13
class g:
14
  def forward(self, x):
15
    self.x = x
16
    return g(x)
17
  
18
  def backward(self, d_out):
19
    return dg(self.x) * d_out
20
  
21
  def dg(self):
22
    return central_difference(f, self.x)

So, to cauculate the $f'_x(g(x))$ value, and the d_out passed to backward of the first box should be the value returned by the backward of the second box. The 1 at the end is to start off the chain rule process with a value for d_out.

Now, let's see an example. Suppose we want to calculate the derivate of $f(g(x)) = sin(x^2)$ at $x = 3$. Based on chain rule, we can derive that,

As we have defined square class, now we have to define the sine class. Note that we use symbolic derivatives for $g(x) = x^2$ and numerical derivatives for $f(x) = sin(x)$ in order to show both of these methods. So now these classes should be defined as,

xxxxxxxxxx
29
1
class square:
2
    
3
    def __init__(self, x):
4
        self.x = x
5
        return
6
    
7
    def forward(self):
8
        return self.x**2
9
    
10
    def backward(self, d_out):
11
        return self.dsquare() * d_out
12
    
13
    def dsquare(self):
14
        return 2 * self.x
15
​
16
class sine:
17
    
18
    def __init__(self, x):
19
        self.x = x
20
        return
21
    
22
    def forward(self):
23
        return np.sin(self.x)
24
    
25
    def backward(self, d_out):
26
        return self.dsine() * d_out
27
      
28
    def dsine(self):
29
        return central_difference(np.sin, self.x)

Then we can have the forward pass as,

xxxxxxxxxx
1
1
print(sine(square(3).forward()).forward())

And the output should be 0.4121.

Also, the backward pass is calculated as,

xxxxxxxxxx
1
1
print(square(3).backward(sine(square(3).forward()).backward(1)))

This result of -5.4668 matches the value we have calculated by chain rule.

(3) Backpropagation

The backward function tells us how to compute the derivastive of one operation, and the chain rule tells us how to compute the derivative of two sequential operations. For backpropagation (aka. Backprop), it is going to show us how to use these rules to compute a derivative for an arbitrary series of operations.

Now, let's suppose we have two arguments $x$ and $y$ and a function $h(x, y)$ defined as follows,

Let's suppose we would like to compute the derivatives of $h'_x(x, y)$ and $h'_y(x, y)$. Then based on the $h(x, y)$ function we have defined, we can construct a box graph as follows,

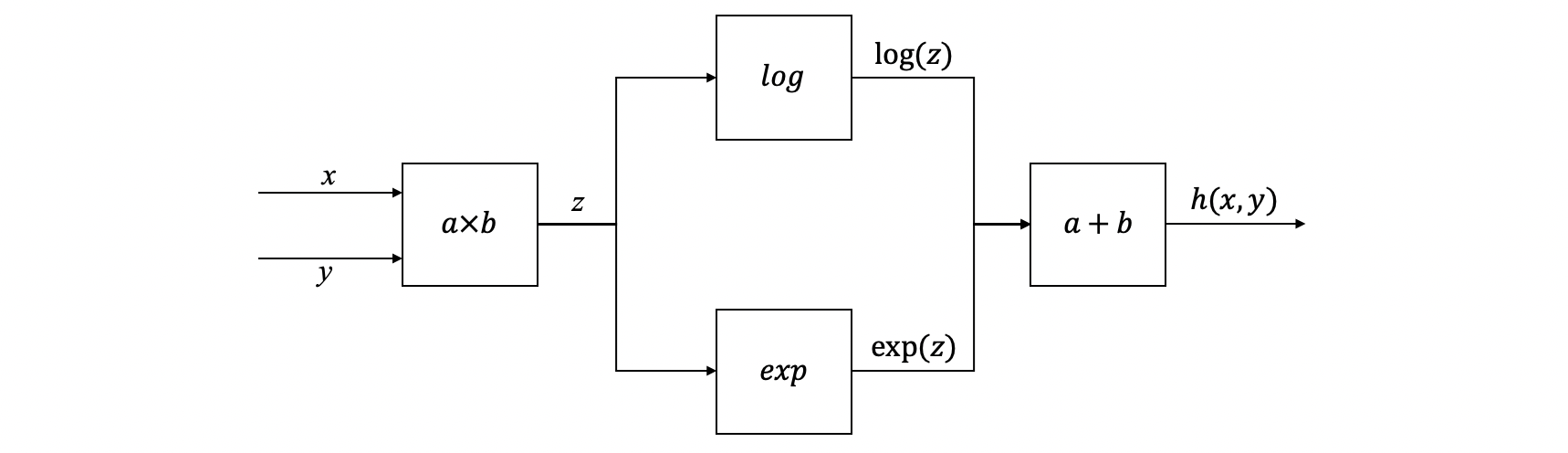
Based on the chain rule, we have,

Then let's consider the backpropagation. From right to left, we have d_out = 1 as an initial backward input. According to the derivatives of $a + b$ on $a$ and $b$ are both 1, the first step backward pass got 1s for as the d_out input for the next step.

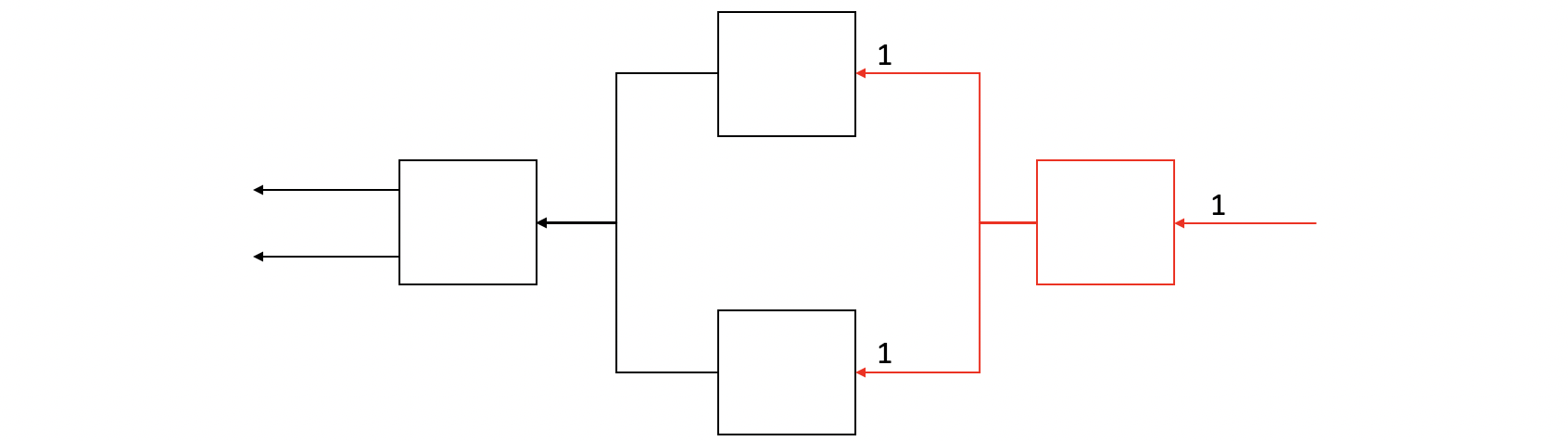
Then, let's suppose we first compute the backward of the $log$ function. From the backward method we have discussed, the result of this step should be computed as,

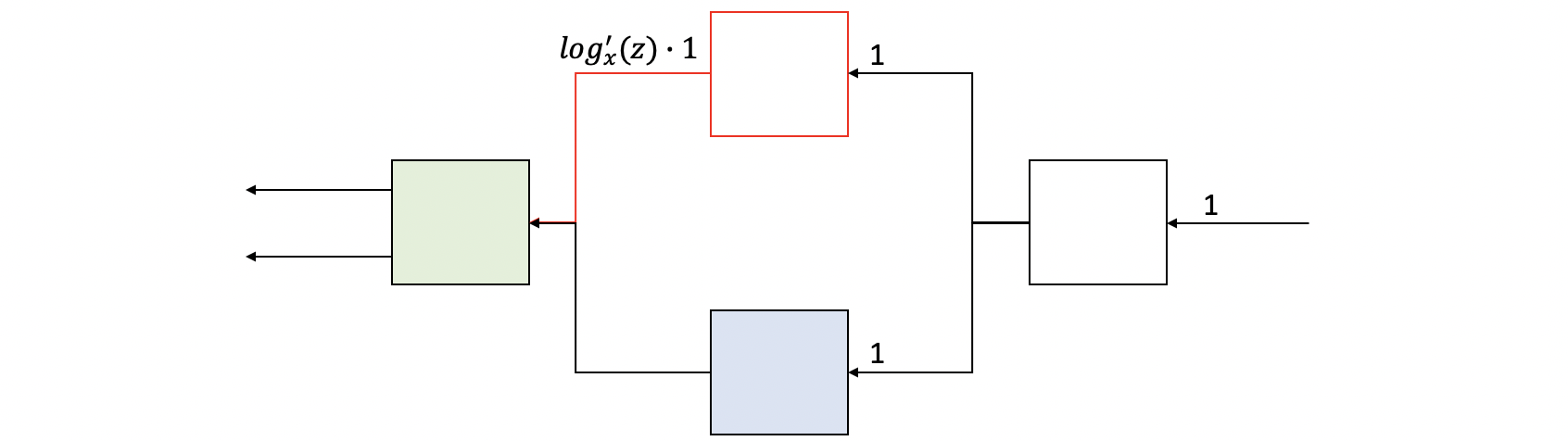
So the next issue is that, it sames that we can continue to backward to both the green box and the blue box, but the order of the backward pass really matters. Actually, in this case we have to perform the blue box as the next backward step instead of the green one, but how can the machine know that?

(4) Topological Sort

To handle this issue, we will process te nodes in a topological order. Firstly, we have to note that our graph is not a random directed graph, it is actually a DAG (aka. Directed Acyclic Graph). Please refer to this article if you can not remember clearly what a DAG is. In this case, the direcionality comes from the backward function and the lack of cycles is a consequence of the choice that every function must create a new variable.