Data Structure and Algorithm 2 | Dynamic Connectivity Problems

1. Union Find

(1) Functions

• union: Used to connect two objects.
• connected: Used to check is there a path connecting the two objects.

(2) The Definition of Connection

We can assume that the connected is defined as the following relations,

• Reflexive: p is connected to p
• Symmetric: If p is connected to q, then q is connected to p
• Transitive: if p is connected to q and q is connected to r, then p is connected to r

(3) The Definition of Connected Components

The connected components are defined as the maximal set of objects that are manually connected. For example, the following connected graph has the connected components of { 0 } { 1 4 5 } { 2 3 6 7 }.

(4) Union-Find API

• Initialize union-find data structure with N objects

1
UF(int N)

• Add connection between p and q

xxxxxxxxxx
1
1
void union(int p, int q)

• Check if p and q are in the same component

xxxxxxxxxx
1
1
boolean connected(int p, int q)

• Component Identifier for p (0 to N-1)

xxxxxxxxxx
1
1
int find(int p)

• Get the number of components

xxxxxxxxxx
1
1
int count()

(5) Dynamic Connection Client

Before we discuss our client, let's first have a look at our input. The tinyUF.txt file starts with an integer N meaning the number of objects we have. Then, it comes with pairs of integers that shows us the connectivity repationships of the objects.

xxxxxxxxxx
12
1
10
2
4 3
3
3 8
4
6 5
5
9 4
6
2 1
7
8 9
8
5 0
9
7 2
10
6 1
11
1 0
12
6 7

Then, the client of our dynamic connection instance is as follows. It reads in number of object N from standard input and then repeat in pairs of integers from the standard input and connect them with the UF API we have provided. If two objects have not yet been connected, then the client will connect them and print out the pairs.

​x
1
import edu.princeton.cs.algs4.StdIn;
2
import edu.princeton.cs.algs4.StdOut;
3
​
4
public class DynamicConnectClient {
5
    public static void main(String[] args) {
6
        int N = StdIn.readInt();
7
        UF uf = new UF(N);
8
        while (!StdIn.isEmpty()) {
9
            int p = StdIn.readInt();
10
            int q = StdIn.readInt();
11
            if (!uf.connected(p, q)) {
12
                uf.union(p, q);
13
                StdOut.println(p + " " + q);
14
            }
15
        }
16
    }
17
}

Based on the definition of connectivity, the object pairs 8 9, 1 0, and 6 7 would be automatically connected so they should not be printed out in the result.

2. Quick-Find

(1) Quick-Find Algorithm

Quick-find an eager approach (means that it will rewrite in every update) is to assign each object in the same comonent with the same id stored in an interger array id[]. Object p and q are connected if and only if they have the same id. For finding if p and q are connected, the find method will check if p and q have the same id.

xxxxxxxxxx
28
1
public class QuickFindUF {
2
    private int[] id;
3
​
4
    public QuickFindUF(int N) {
5
        id = new int[N];
6
        for (int i = 0; i < N; i++)
7
            id[i] = i;
8
    }
9
​
10
    public boolean connected(int p, int q) {
11
        return id[p] == id[q];
12
    }
13
​
14
    public void union(int p, int q) {
15
        int pid = id[p];
16
        int qid = id[q];
17
        for (int i = 0; i < id.length; i++)
18
            if (id[i] == pid) id[i] = qid;
19
    }
20
​
21
    public int find(int p) {
22
        return id[p];
23
    }
24
​
25
    public int count() {
26
        return id.length;
27
    }
28
}

(2) Quick-Find Performance

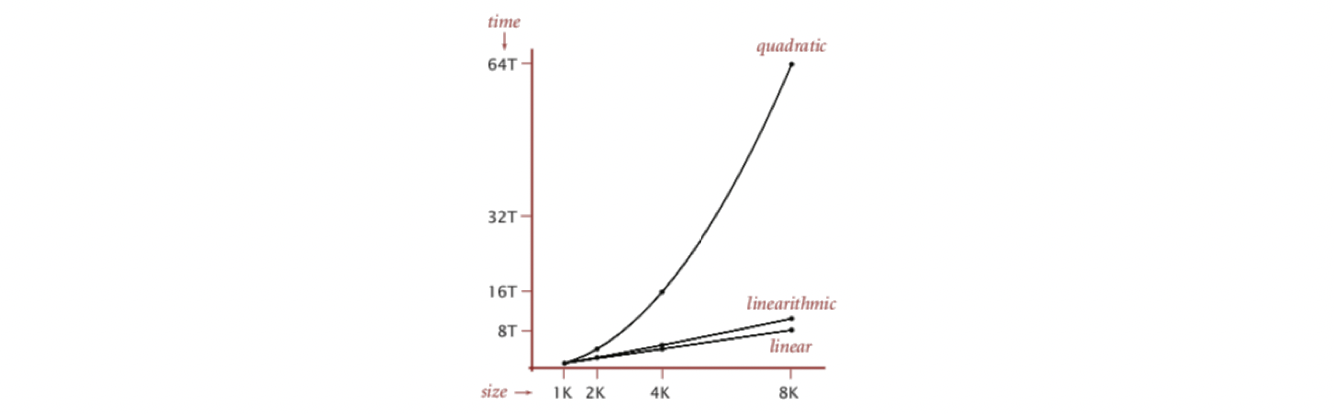
Because quick-find is an eager algorithm, it can be too slow and expensive. It takes O(N) for initialization and O(N) for the union. It takes the cost of even O(N²) to process a sequence of N union commands on N objects. It should also be mentioned here that the cost of finding an object is only O(1), which is preferred. However, because we have a quadratic complexity of union, computing time can be a huge problem.

For example, suppose we have 10⁹ union objects, the quick-find algorithm would take more than 10¹⁸ operations, this means over 30 years of computing time.

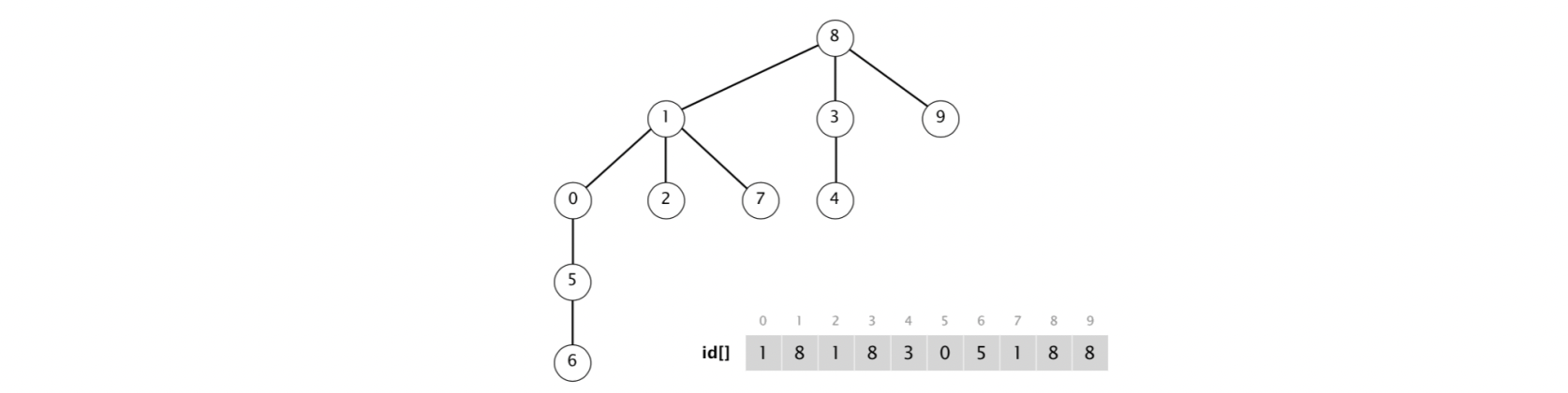
3. Quick-Union

(1) Quick-Union Algorithm

Quick-union is a lazy approach that will save the work until the task is called. Similarly, we have an integer array id[] of length N, and the id[i] for object i is the parent of i, so

xxxxxxxxxx
1
1
id[i] = parent(i)

Then,

xxxxxxxxxx
1
1
id[id[i]] = parent(parent(i))

Continue this process, we have,

xxxxxxxxxx
1
1
id[id[id[id[...i...]]]] = root(i)

Because we initialize the id array with each i itself, the root should satisfy,

xxxxxxxxxx
1
1
root(r) === r

Therefore, to unite to objects, we only need to assign the root of the second object as the parent of the root of the first object.

xxxxxxxxxx
1
1
id[root(p)] = root(q)

Also, in order to check if two objects are connected, we only need to check if the roots of them are equivalent.

xxxxxxxxxx
1
1
root(p) == root(q)

Therefore, the class QuickUnionUF should be defined as,

xxxxxxxxxx
33
1
public class QuickUnionUF {
2
    private int[] id;
3
​
4
    public QuickUnionUF(int N) {
5
        id = new int[N];
6
        for (int i = 0; i < N; i++)
7
            id[i] = i;
8
    }
9
​
10
    private int root(int p) {
11
        while (p != id[p])
12
            p = id[p];
13
        return p;
14
    }
15
​
16
    public boolean connected(int p, int q) {
17
        return root(p) == root(q);
18
    }
19
​
20
    public void union(int p, int q) {
21
        int pid = root(p);
22
        int qid = root(q);
23
        id[pid] = qid;
24
    }
25
​
26
    public int find(int p) {
27
        return root(p);
28
    }
29
​
30
    public int count() {
31
        return id.length;
32
    }
33
}

The result of Quick-Union should be a data structure of the tree. For example,