Java Programming 3 | Array, Coupon Collector Problem, and Self Avoiding Random Walks
Java Programming 3 | Array, Coupon Collector Problem, and Self Avoiding Random Walks

- Array
(1) The Definition of Data Structure
A data structure is an arrangement of data that enables efficient processing by a program.
(2) The Definition of Array
An array is an indexed sequence of values of the same type. The main purpose of an array is to facilitate storage and manipulation of data.
- Indices start at 0
- Given i, the operation of accessing the value a[i] is extremely efficient
- The assignment b = a makes the names b and a reference to the same array
(3) Initialization Options
- Default initialization to 0 for numeric types, for example,
a = new double[1000];
- Declare, create and initialize in one statement
double[] a = new double[1000];
- Initialize to literal values
double[] x = { 0.3, 0.6, 0.1 };(4) Basic Supports For Array
- Declare an array
double[] a;
- Create an array of a given length
a = new double[1000];
- Refer to an array entry by index
a[i] = b[j] + c[k];
- Refer to the length of an array
a.length;
(5) Copying an Array
The code b = a does not copy an array (it makes b and a reference to the same array). To copy an array, create a new array, then copy all the values. So we have to assign the element one by one,
double[] b = new double[a.length];
for (int i = 0; i < a.length; i++) b[i] = a[i];
If we use b = a, then we can get the same array,
0 1 2 3 4 5
0 1 2 3 4 5
2. Array: Examples
(1) Create a Deck of Cards
Use nested for loops to put all the cards in the deck.
(2) Take a Card, Any Card
Algorithm: Take N from the command line and do the following N times
- Calculate a random index r between 0 and 51
- Print deck[r]

Note that the sample is with replacement (the same card can appear multiple times).
(3) Shuffle and Deal
Suppose we want to shuffle the desk first and then deal with the desk in order. The algorithm should be,
- Consider each card index i from 0 to 51
- Calculate a random index r between i and 51
- Exchange deck[i] with deck[r]
- Print the first N cards in the deck
(4) Coupon Collector Problem
Suppose that we want to have a collection of the coupon and this must be composed by M different coupons in the deck (2 to A). We can conduct this experiment for N times and then calculate the average times we need to get a collection of M coupons.
In practice, this question is equivalent to the question that, suppose we want to collect a series of cards as a coupon of a kind of product, and by opening one bag of the product, we can get 1 card per bag. Suppose that there are in total M different cards and we want to collect them all. And the probability of each card in the bag is equal. So how many trials we can have to attempt to get a whole selection of the cards?
We are not going to go too detailed for this example. What are we going to do is to give us the solution to this problem directly. Based on the Euler–Mascheroni constant, we can then have the conclusion the expectation of the attempts should be,
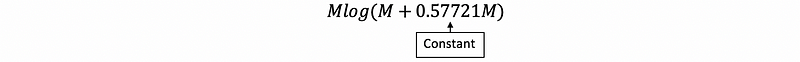
In our code, we are going to have two parameters, the first one is the numbers of the coupons M, the second one is trials of the experiment N. We are going to print three results, real mean attempts for M coupons after N trials, the estimated expectation attempts by Euler–Mascheroni constant, and finally the error between these two values.
We can test the result for M = 4, 13, 100, and more (with 100 trials) …
- M = 4
4 coupons for mean attempts = 7
Estimated result based on Euler–Mascheroni constant = 7.367807297884452
Error Value = 0.3678072978844522
- M = 13
13 coupons for mean attempts = 39
Estimated result based on Euler–Mascheroni constant = 39.267888670565874
Error Value = 0.26788867056587407
- M = 100
100 coupons for mean attempts = 505
Estimated result based on Euler–Mascheroni constant = 506.08276493393134
Error Value = 1.0827649339313439
3. Two-Dimension Array
(1) The Definition of A Two-Dimension Array
A two-dimensional array is a doubly-indexed sequence of values of the same type. The main purpose of the two-dimension array is to facilitate the storage and manipulate data. Java language support for two-dimensional arrays.
(2) Initialization Options
- Default initialization to 0 for numeric types
a = new double[1000][1000];
- Declare, create and initialize in a single statement
double[][] a = new double[1000][1000];
- Initialize to literal values
double[][] p =
{
{ .92, .02, .02, .02, .02 },
{ .02, .92, .32, .32, .32 },
{ .02, .02, .02, .92, .02 },
{ .92, .02, .02, .02, .02 },
{ .47, .02, .47, .02, .02 },
};
(3) Basic Operations
- Declare a two-dimensional array
double[][] a;
- Create a two-dimensional array of a given length
a = new double[1000][1000];
- Refer to an array entry by index
a[i][j] = b[i][j] * c[j][k];
- Refer to the number of rows
a.length;
- Refer to the number of columns
a[i].length;
- Refer to row i
a[i]
Note that there’s no way to refer directly to column j.
(4) Vector and Matrix Calculations
- Vector Addition
double[] c = new double[N];
for (int i = 0; i < N; i++)
c[i] = a[i] + b[i];
- Matrix Addition
double[][] c = new double[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
c[i][j] = a[i][j] + b[i][j];
- Vector Dot Product
double sum = 0.0;
for (int i = 0; i < N; i++)
sum += a[i]*b[i];
- Matrix Multiplication
double[][] c = new double[N][N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
for (int k = 0; k < N; k++)
c[i][j] += a[i][k] * b[k][j];
(5) Two-Dimension Array: Self Avoiding Random Walks
So our model here is a random process in an N-by-N lattice followed by the steps:
- start in the middle
- move to a random neighboring intersection but do not revisit any intersection
- Escape: reach edge of the lattice
- Dead end: No unvisited neighbors
To try this code, we can then have the result as,
10 by 10 lattice with 5% dead ends for 1000000 trials.
20 by 20 lattice with 32% dead ends for 1000000 trials.
30 by 30 lattice with 59% dead ends for 1000000 trials.
40 by 40 lattice with 77% dead ends for 1000000 trials.
50 by 50 lattice with 87% dead ends for 1000000 trials.
60 by 60 lattice with 93% dead ends for 1000000 trials.
70 by 70 lattice with 96% dead ends for 1000000 trials.
80 by 80 lattice with 98% dead ends for 1000000 trials.
90 by 90 lattice with 99% dead ends for 1000000 trials.
100 by 100 lattice with 99% dead ends for 1000000 trials.
This result has many physical applications (solvents, polymers, magnetic materials, etc.) and the probability of reaching a dead hasn’t been solved by the mathematicians and the physics researchers despite decades of study. But we can clearly see from our program that when N > 100, the probability of dead ends is greater than 99%.