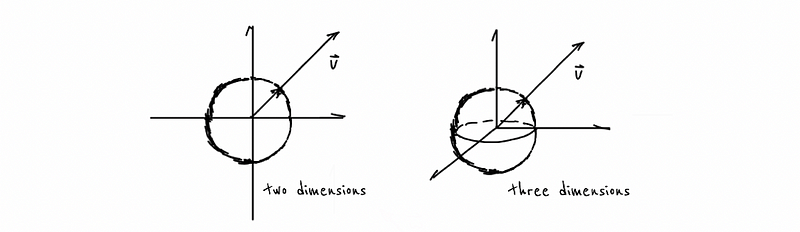
Linear Algebra 1 | Euclidean Space, Vectors, and Dot Product

Linear Algebra 1 | Euclidean Space, Vectors, and Dot Product

1. Euclidean Space

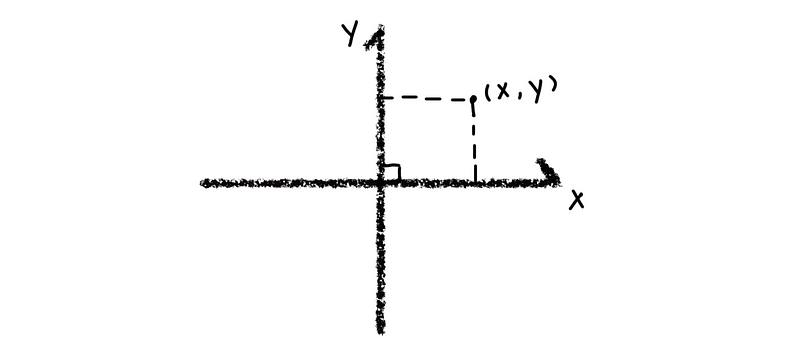
ℝ², which is the most common Euclidean Space, represents the set of all ordered pairs of real numbers. For example, the pair of numbers as (x, y).

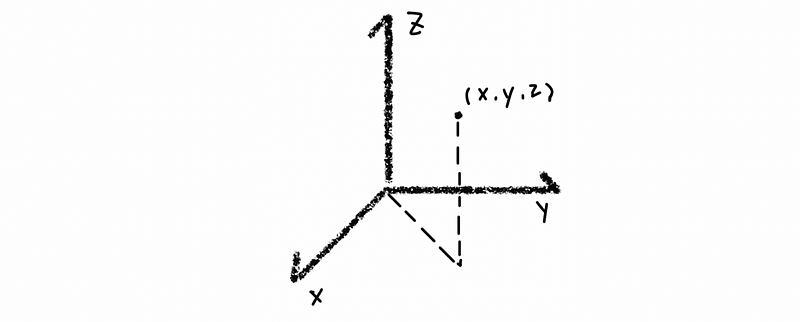
It is quite similar when we talk about ℝ³, which represent the set of all ordered collection with three real numbers. For example, (x, y, z).

(1) Vectors

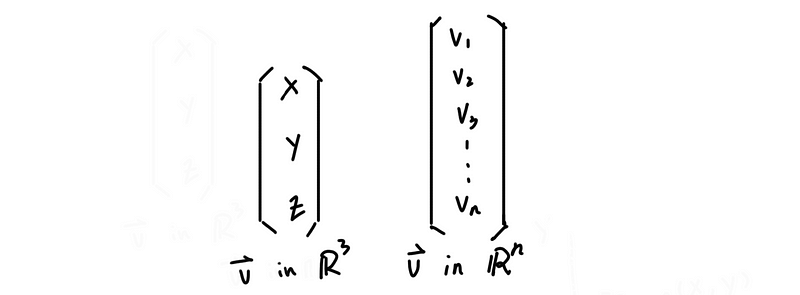
Here we have a column vector in ℝ², which is an abstract arrow emanating from Origin (0, 0) and pointing towards the point (x, y). Each of the numbers in this vector is called a component. So in this case, we have got two components, which are component x and component y.

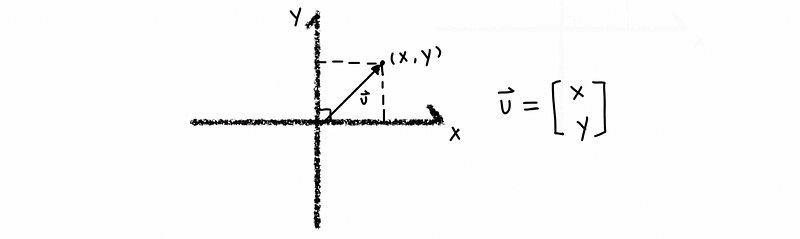
Similarly, vectors in ℝ³ and vectors in ℝⁿ have the expended structure compared with the vector in ℝ².

(2) Vector Space

A place where we can add vectors or multiply vectors by numbers. ℝⁿ is our canonical example of a vector space.

We can simply add two vectors together by adding up each of the components.

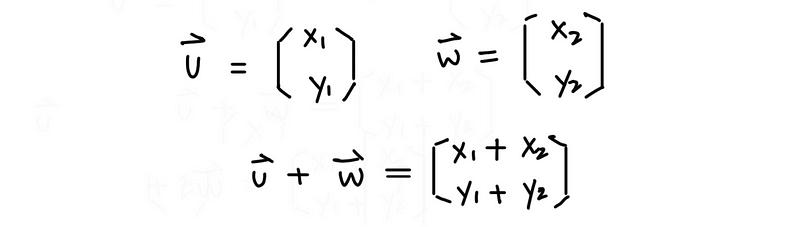
(3) Scalars

When we talk about multiplying the vector by a number, often, we call them scalars. They have to be real numbers. If we use a scalar to multiple the vector, the result equals to we multiple every component with this scalar. Geometrically, the scalar changes the length of the vectors.

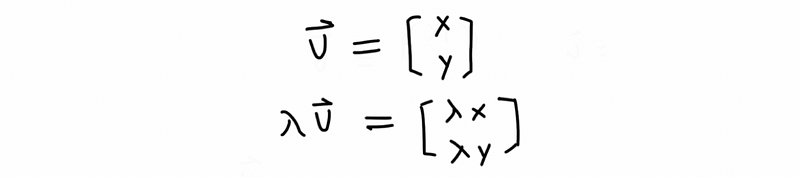
(4) Vector Geometry

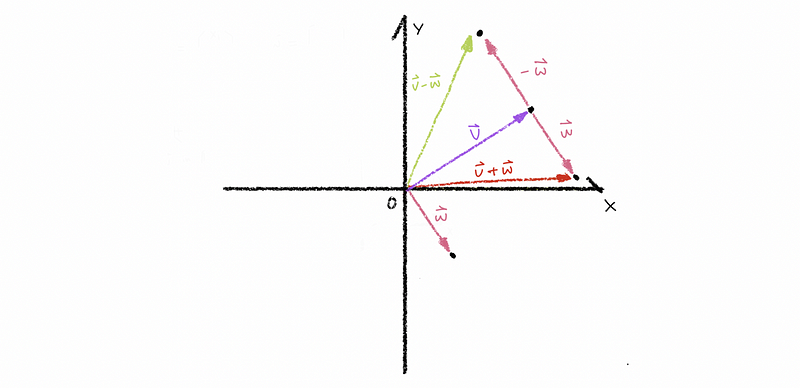
Say if we have vector v and vector w, we can add them up or minus them to get new vectors. But what’s the meaning of the new vector v + w or v - w in geometry? The following picture shows the geometric meaning of these two results.

(5) Properties of the Vectors

There are mainly three properties that we should remember. The letters represented in bold and tilt pattern are treated as vectors.

• u + (- u) = 0
• (c + d) v = cv + dv
• c (v + w) = cv + cw

2. Linear Combinations of Vectors

(1) Linear Combination

If we have a set of vectors {v₁, v₂, v₃, …, vn} and constants c₁, c₂, c₃, …, cn (or we called scalars, ci ∈ℝ), we can form linear combinations.

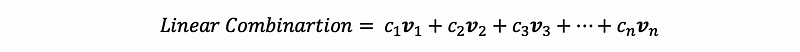
(2) Linear Combination of a Vector

The geographic meaning of linear combinations of a vector is on a line in the Euclidean Space.

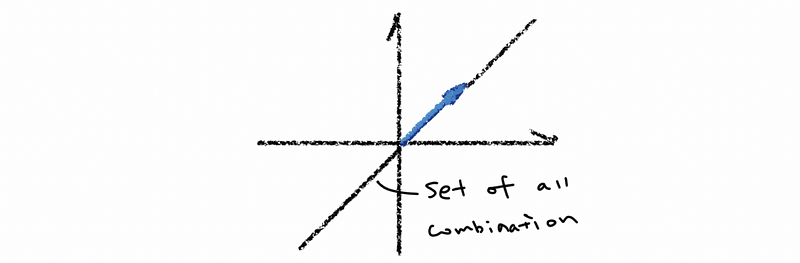
(3) Linear Combination of two Vectors

The geographic meaning of linear combinations of a vector is on a plane in the Euclidean Space.

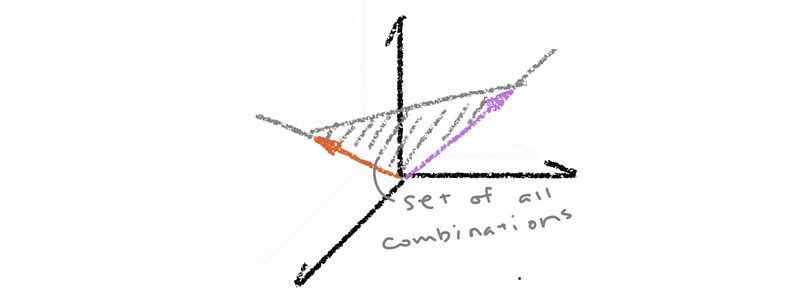
(4) Dot Product (aka. inner product)

Suppose we have vector v and vector w in ℝⁿ space. So the result of v · w follows the following equation.

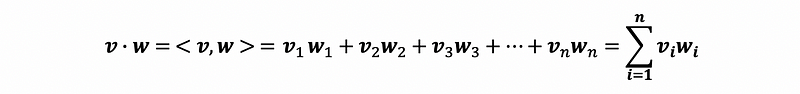
in which, the meaning of <,> is ℝⁿ · ℝⁿ → ℝ.

(5) Length of the Vector (aka. norm)

We can calculate the length of the vector through the definition of the dot product. The length of a vector equals the square root of the vector dots itself. For example,

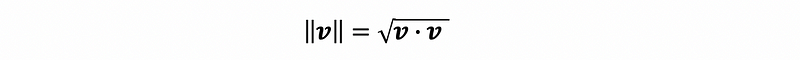
(6) Orthogonal (aka. perpendicular) Vectors

If the dot product of two vectors equals zero, so these two vectors are orthogonal vectors, which geometrically means that they are on two perpendicular lines. For example,

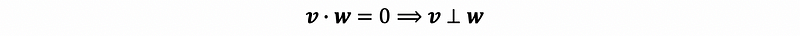
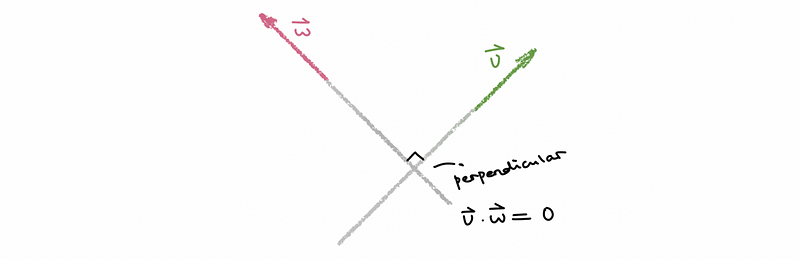
(7) Linear Combination and Orthogonal Vectors

Obviously, the linear combinations of orthogonal vectors (# equals the dimensions) give all of the space.

(8) Law of Cosines

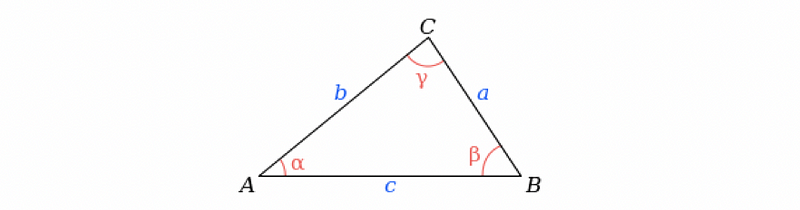
The law of cosines reveals the relationship between the three sides of a triangle. The law is as follows:

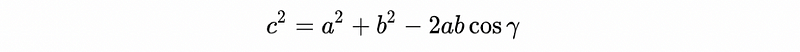
while γ is the angle between the side a and side b. It could be proved with the properties of the trigonometric functions.

(9) Law of Cosines on Vectors

Suppose we have the vector V₃ equals to the vector V₁ plus the vector V₂. So the law of cosines on vectors could be applied as follows:

(10) The Geometric Form of Dot Product

Therefore, based on what we have achieved, we can have the conclusion that,

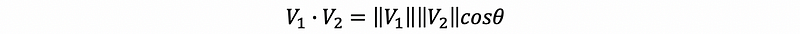
This equation shows the geometric form of the dot product.

(11) Unit Vector

If the length of a vector equals 1 (or as we say norm = 1), this vector is so-called the unit vector. To find a vector’s unit vector in the same direction, we can divide the vector with its norm. For example, in the following equation, the vector u is a unit vector of the vector v.

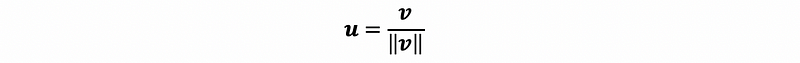
(12) United Vector and Cosine

Based on what we have proved in the previous part, we have already had the result of:

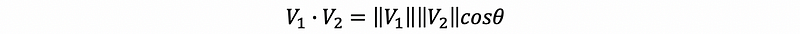
If we divide the norm to both hand sides, we will have a new expression as follows,

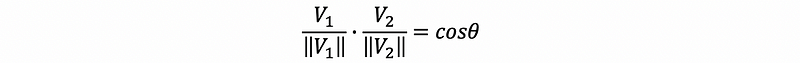
which is also,

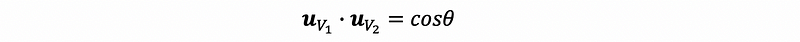
So the dot product of the unit vector on the vector V₁ and V₂ equals the cosine values of their included angle.

(13) The Set of the Unit Vector