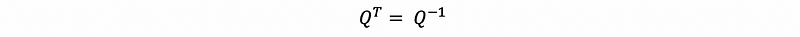Linear Algebra 6 | Full Rank, Projection Matrix, And Orthogonal Matrix
Linear Algebra 6 | Full Rank, Projection Matrix, And Orthogonal Matrix
- Full Rank
(1) The Definition of Full Rank
Suppose that the matrix A has a shape of m × n. Then the rank of matrix A is constrained by the smallest value of m and n. We say a matrix is of full rank when the rank is equal to the smaller of m and n, which also means that the rank should be as big as it can be.
For example, let’s look at a tall skinny matrix A with shape m × n (m > n),
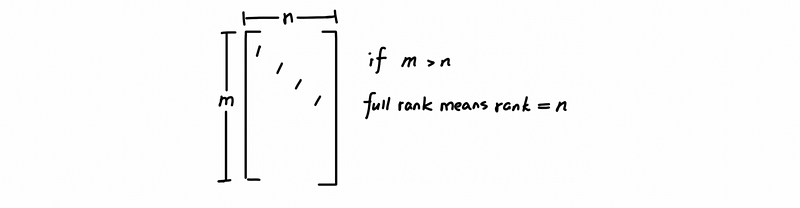
(2) The solutions of a Full Rank Matrix
For any matrix A with full rank, suppose we want to solve our friend Ax = b, you can have either a 0 solution or you can barely have one unique solution. We can never have infinite solutions and this is because all the columns in A are linearly independent. So once you find a solution of a full rank matrix, there’s nothing you can add to it from the space to get new solutions, or you could also have no solution.
2. A Practical Case
(1) Plan Ticket Application
I bet the price of a plane ticket to San Francisco is a function of distance, so the longer the miles, the more expensive the ticket is. And because I am a lazy guy and I don’t want to make the things difficult, so I just assume that the relationship between the ticket price and the distance is linear.
Now let’s gather some data, maybe from newspapers or websites, whatever, and we get a bunch of data that can be helpful for our modeling. For the distances we have x1, x2, …, xn, and for the prices, we have y1, y2, …, yn. These are all real values and we can have a list or table of these data like,
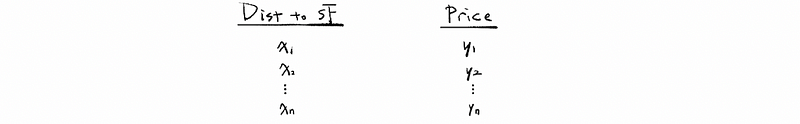
As we believe our model is a linear model, we can then have a basic model as,
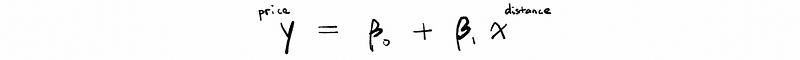
If I am exactly correct on this model, we can then have a bunch of equations as,
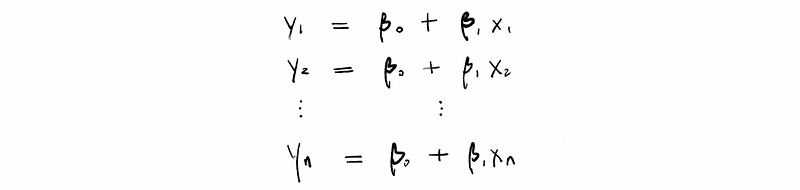
And our model holds for all these data.
However, because we don’t like the system of equations and we just want to use the matrix equation, so we can then rewrite this system of equations to something that can be represented by matrix:
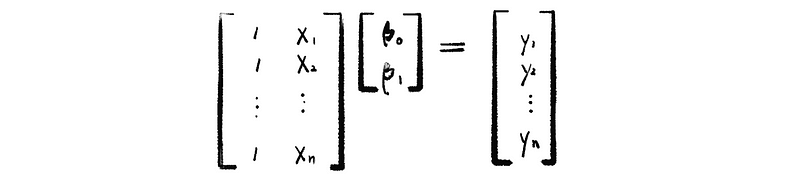
Because we have only 2 coefficients but we can have as many data as we want to have, so it is quite unlikely that we can find out a solution of [β0, β1] that can solve this equation system. So what’s the best thing we can do?
Now, let’s assume the matrix A and the vector y,
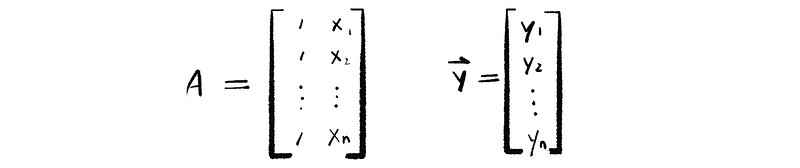
So based on our observation, the vector y is probably not in the column space of A ( Col(A) ) and this means that this equation system will have no solution.
(2) The Best Thing We Can Do
Find a vector in Col(A) that is as close as possible to the vector y. This is because we can hardly find a vector y that is in the column space of A.
Now we define the
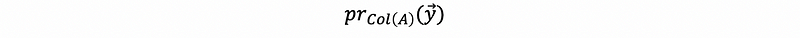
as a projection of vector y onto the subspace Col(A), geometrically,
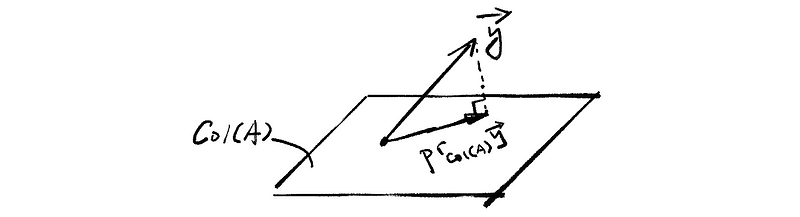
Let’s suppose,
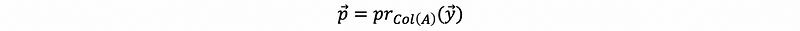
minimizes the distance to y, so based on its definition, we can then have two observations as,
- Observation #1: Orthogonality
Because we have to choose a vector p satisfies,
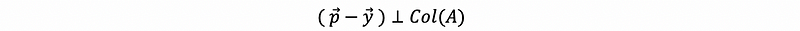
And by what we have talked about in the last part, we have,
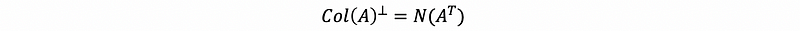
so,
- Observation #2: Minimization-this has the same meaning as the orthogonality
Because p minimizes the distance to y, which is also to say that, for all
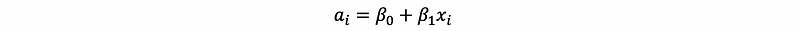
we have p minimizes,
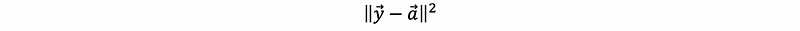
and because that,
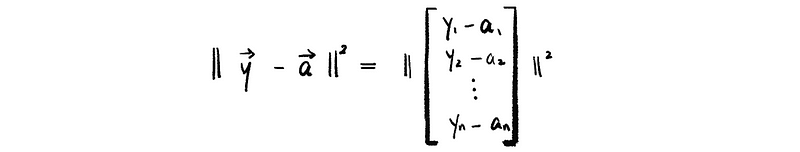
then,
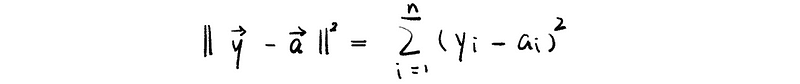
thus, we are to find,
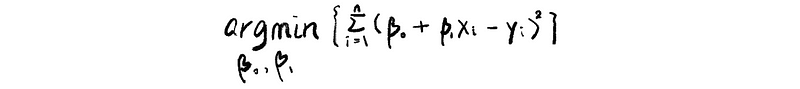
(3) Start With One-Dimension Version
Suppose the column space of A has only one dimension, we can find the projection of vector y onto the Col(A) = span{w}.
We can then define,
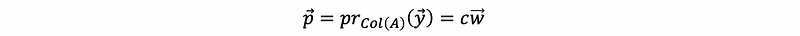
by observation #1, we make,
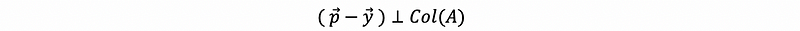
then,
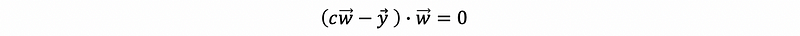
then,
then,
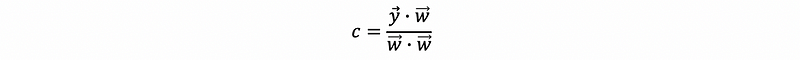
thus,
(4) A More General Version
Suppose we have a vector y and we want to find its projection vector in the subspace of Col(A), it is then shown by the following graph as,
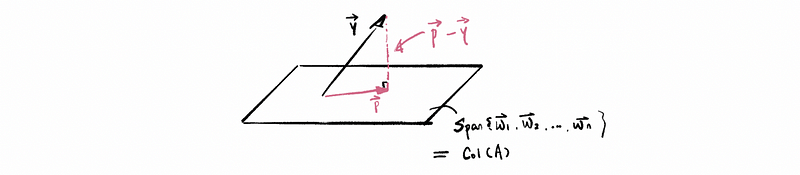
So then because our goal is to find the best approximate to y that live in Col(A), let’s go ahead and say that {w1, w2, …, wn} is a basis for Col(A) if we let,
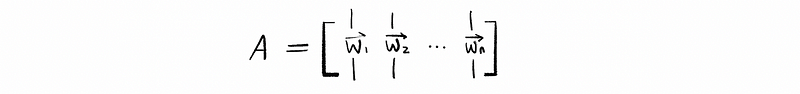
so our basic idea is that,
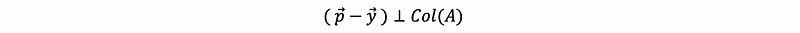
As we have proved that,
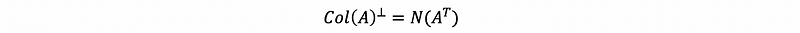
so p-y must live in the null space of A transpose, which is also,
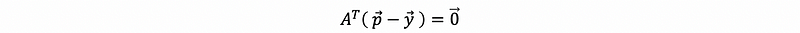
And because p is in the subspace of Col(A), then, ∃ some vector x ∈ A that satisfies,
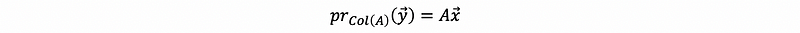
then we have,
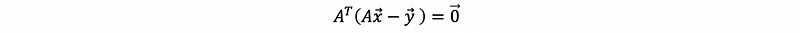
so,
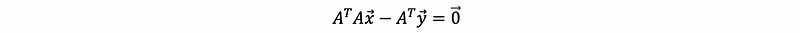
then,
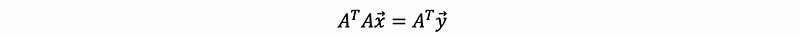
and because A^TA is invertible (we will prove this in the following part), so then,
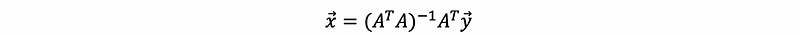
remember that,
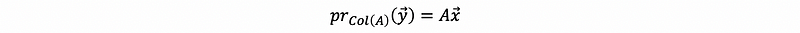
thus,
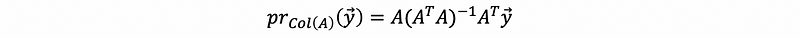
3. Projection Matrix
(1) The Definition of The Projection Matrix
By the previous discussion, we discover that the matrix P which equals,
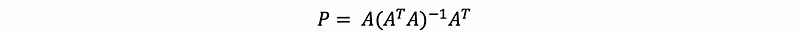
and this matrix transfers a vector in ℝᵐ to the Col(A) and P: ℝᵐ → ℝᵐ. So we call this matrix P as a projection matrix to subspace Col(A).
(2) A Property of The Projection Matrix
It is quite clear to find out that because any vectors will exactly equal to themselves if they are already in the subspace Col(A), so that,
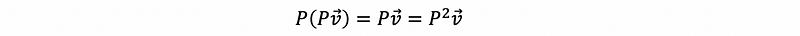
thus,
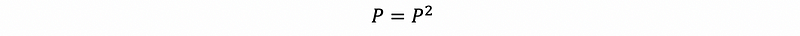
Generally, it is quite clear that,
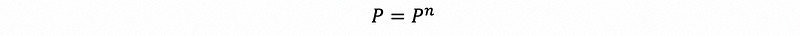
(3) Think Back on One-Dimension Version
Based on our discussion in the one dimension Col(A), we can know that when the dimension of matrix A equals one, then,
because w is a vector, then,
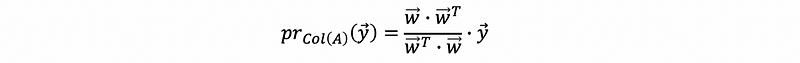
so that we can have a projection vector as,
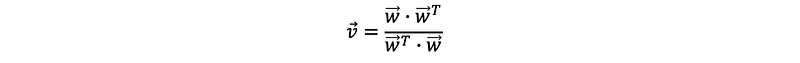
(4) Loose End: We have to Prove that A^TA is invertible
If we want to prove that A^TA is invertible, it is equal to prove that:
- A^TA is a square matrix
- whichever pairs of columns in A are linearly independent
Proof:
Let’s suppose our matrix A is an m × n matrix, then,
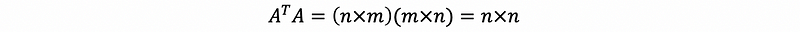
so A^TA must be a square matrix.
Then if we want to prove that all the columns in A are linearly independent, it is equivalent to prove,
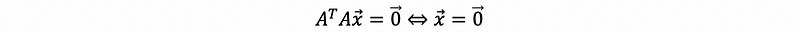
say,
then,
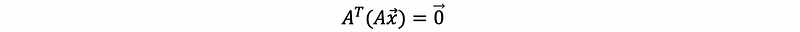
then,
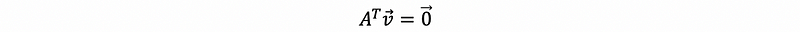
this equals to say that the vector Ax lives in the null space of A transpose,
but also,
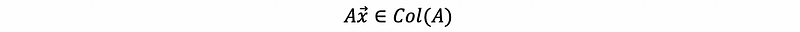
the only way to make this possible is that,
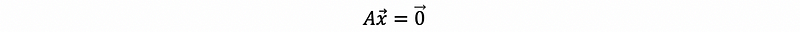
But because the columns in A are linearly independent, we can have,
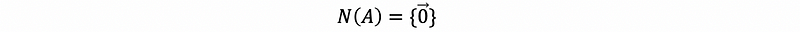
so that,
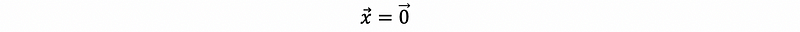
4. Orthogonal Matrix
(1) The Definition of The Orthogonal Basis
Suppose we have a set of vectors {q1, q2, …, qn}, which is orthogonal if,
then this basis is called an orthogonal basis.
(2) The Definition of The Orthogonal Matrix
If in addition, all the vectors are unit vectors if,
then consider a matrix Q whose columns form an orthogonal set as,
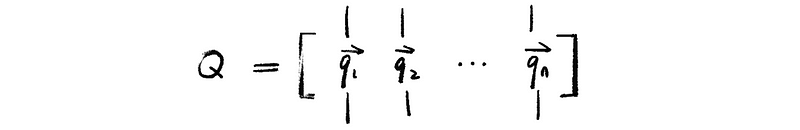
this matrix Q is called an orthogonal matrix.
(3) The Property of The Orthogonal Matrix
Suppose we have matrix Q as an orthogonal matrix, then we can have,
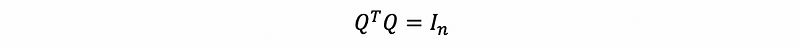
so if Q is a square matrix, then we can have,
