Linear Algebra 7 | Orthonormal Matrix, Orthogonal Transformation, QR factorization, Gram-Schmidt…
Linear Algebra 7 | Orthonormal Matrix, Orthogonal Transformation, QR factorization, and Gram-Schmidt Orthogonalization

- Recall: Least Square Problem
(1) Question
Suppose A is a matrix whose columns are a basis of vector space W ∈ ℝᵐ, so,
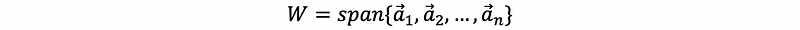
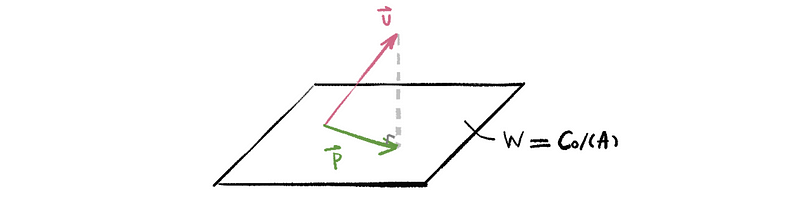
Then we can construct A as an m × n matrix as,
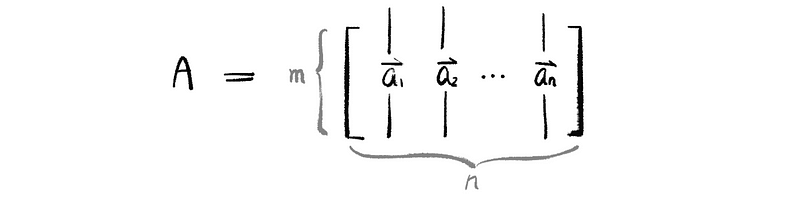
Our goal is to find the best approximation to the vector v in Col(A).
(2) Solution
If we use the normal equation Ax = b, we can have no solution.
So that we can then solve,
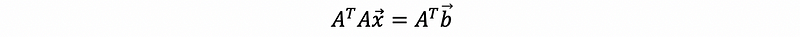
Now, we can have,
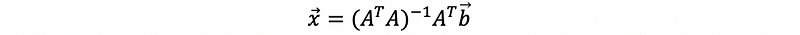
and,
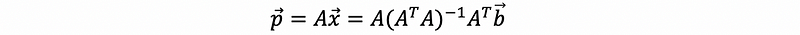
We can also define the projection matrix as,
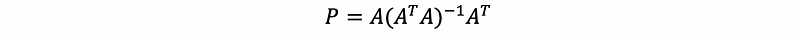
this projection matrix P hits vectors in ℝᵐ and project them into subspace Col(A).
(3) Example
Suppose we have a dataset that (x, y) = {(0, 1), (3, 4), (6, 5)}. And we assume that the model is a linear model as the form of,
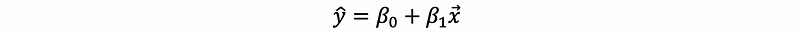
And we would like to find the best fit line in the sense of least squares, which is to minimize,
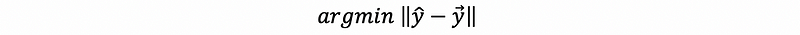
Therefore, we have,
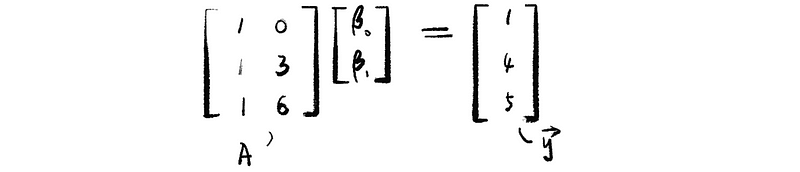
this has no solution, so we rewrite our equation as,
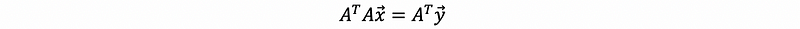
then,
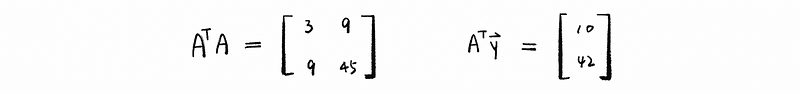
Solve this by,
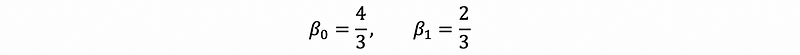
2. Orthogonal Matrix
(1) Orthogonal Basis
Suppose we have a set of vectors {q1, q2, …, qn}, which is orthogonal if,
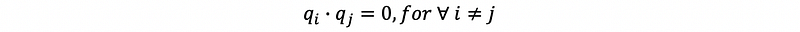
then this basis is called an orthogonal basis. The matrix with its column vectors as orthogonal vectors is called the orthogonal matrix.
(2) Orthonormal Matrix
If in addition, all the vectors are unit vectors if,
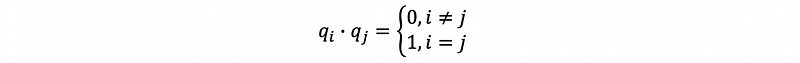
then consider a matrix Q whose columns form an orthonormal set as,
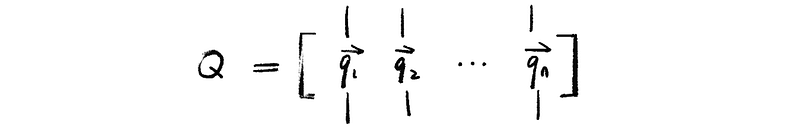
this matrix Q is called an orthonormal matrix. The property of the orthonormal matrix is,
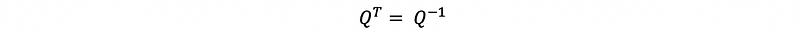
(3) Orthonormal Transformation
If matrix Q has orthogonal columns,
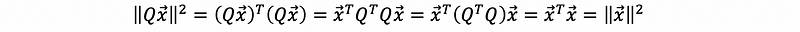
So we can see that the orthonormal matrix Q on x preserves its length.
(4) Orthogonal Transformation: An Example
Suppose we have an orthogonal matrix Q as
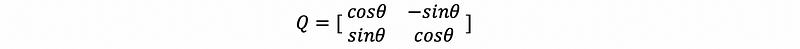
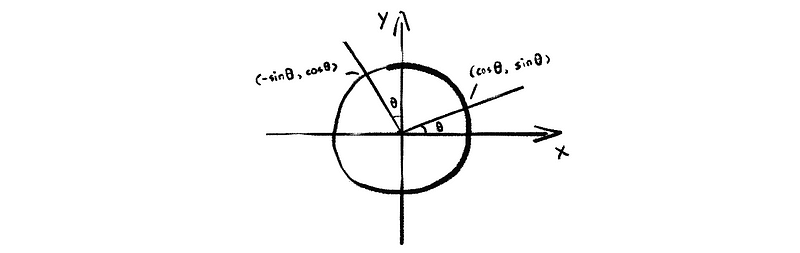
then, we have,

This is also to rotate the vector through angle θ.
(5) Projection Onto Space with An Orthonormal Basis
In our previous case, we discussed that we can project a vector to a vector space Col(A) through a projection matrix P, that is,
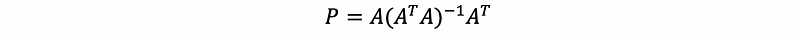
What if the matrix A here is an orthogonal matrix, that is also to say the column space of A has an orthogonal basis. We can use Q to replace A.
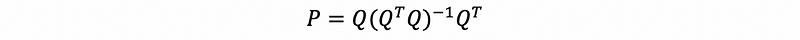
Based on our previous discussion,
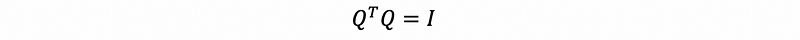
then,
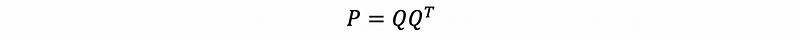
Thus, the projection problem will become a way easier if we are projecting a vector onto a space with an orthogonal basis.
3. Gram-Schmidt Orthogonalization
(1) Projection onto Space with Orthonormal Basis
Suppose we have a vector v and a space Col(Q) with an orthogonal basis {q₁, q₂, …, qn}, then we can project this vector v onto space Col(Q) through,
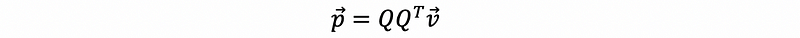
the matrix Q could be written as,
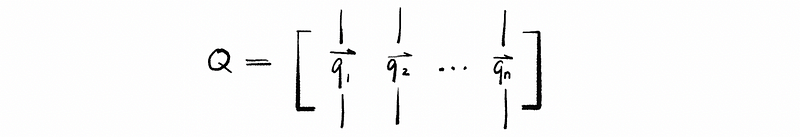
So,
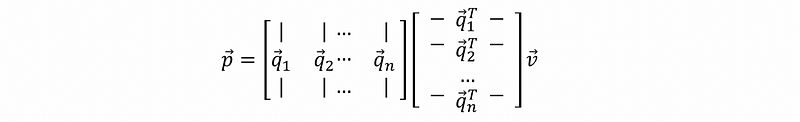
then,
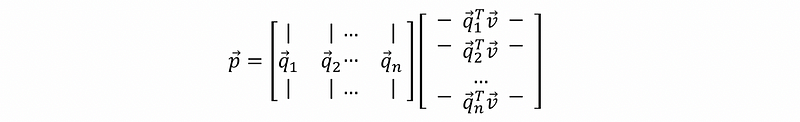
then, this is equivalent to,
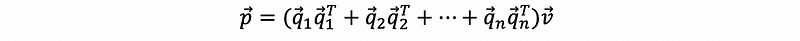
(2) Outer Product
Suppose we have got two vectors x, y in ℝᵐ, then the outer product of these two variables is defined as,
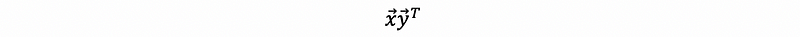
Note that we can compare this with the inner product. The inner product gives us a result of a number, while the outer product gives us a matrix as our result.
(3) Recall: Properties of Vector Product
- Commutative Property
For any vector x, y ∈ ℝᵐ, then we can have the commutative property as,
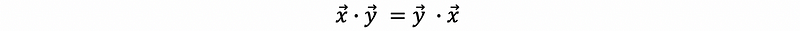
- No Associative Property
For any vector x, y, z∈ ℝᵐ, then we can not have the associative property. Thus,
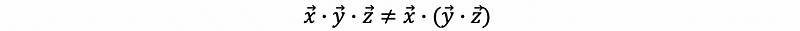
- Commutative Property of Three Vectors
For any vector x, y, z∈ ℝᵐ, then we can have the associative property as,
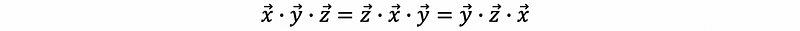
Note that this is different from the associative property.
(4) Projection onto an Orthonormal Vector
If we have the vector w as an orthonormal vector, then we have a vector v that is in the linear combination of w. Suppose that we want to project v onto vector w,
then because w is orthonormal, we can have
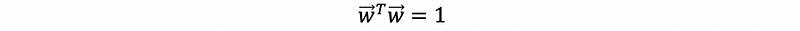
Remember,
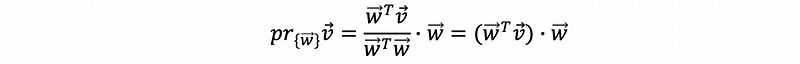
(5) Projection onto an Orthonormal Basis
To project onto space given by an orthonormal basis {q₁, q₂, …, qn}, then we can have,
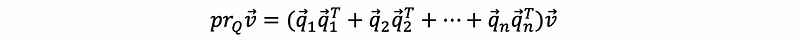
which is also,
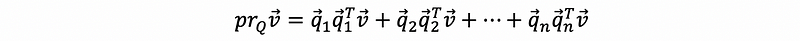
by the commutative property of three vectors,
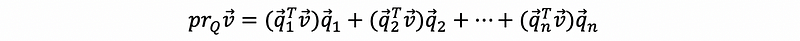
(6) Projection onto Space with Orthogonal Basis
What if we have a basis of {u₁, u₂, …, un} that is orthogonal but not orthonormal? Suppose the columns of matrix U are these orthogonal vectors and in this case, we have the conclusion that,
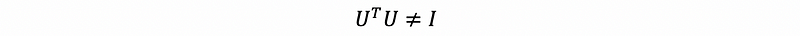
thus,
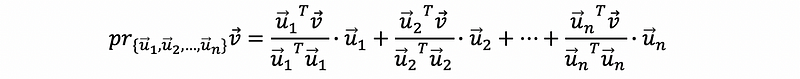
(7) The Definition of Gram-Schmidt Orthogonalization
Suppose given a basis of A as {a1, a2, …, an} in ℝᵐ. Then we produce an orthonormal basis which is {q1, q2, …, qn} satisfies,
- span{a1} = span{q1}
- span{a1, a2} = span{q1, q2}
- ……
- span{a1, a2, …, an} = span{q1, q2, …, qn}
Then if we project a vector onto W = span{q1, q2, …, qn}, this is equivalent to project that onto Col(A) = span{a1, a2, …, an}.
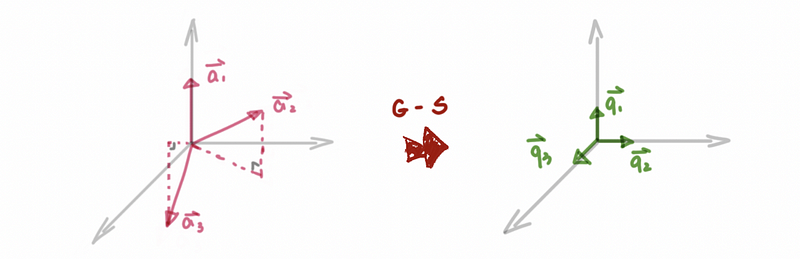
The reason support this orthogonalization is because the vectors space did not change before and after the orthogonalization. The only thing that changes is the basis of this vector space and the basis of a vector space is not unique.
(8) Gram-Schmidt Orthogonalization Process
The G-S process to orthogonalize the a ’s is:
- Normalize a1

- Find q2 by a1
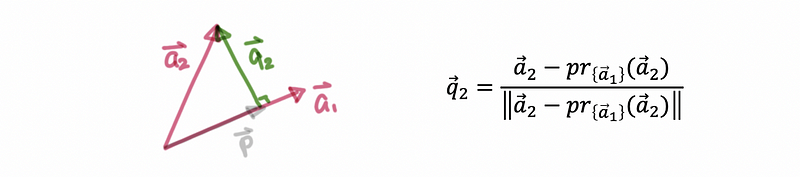
Because q1 = c · a1, then we can have,
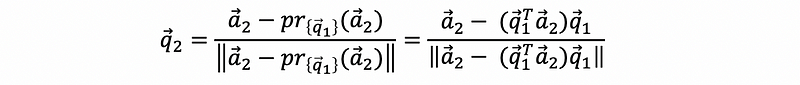
- Continue, find q3 by a1, a2
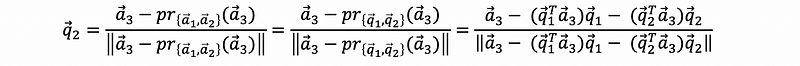
- Continue … until we find the set {q1, q2, …, qn}
(9) QR factorization
By the above discussion, we can find out that we construct a set {q1, q2, …, qn} satisfies,
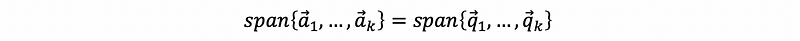
so we can rewrite each the vector ai in the form of the linear combination of {q1, q2, …, qn}, which is,
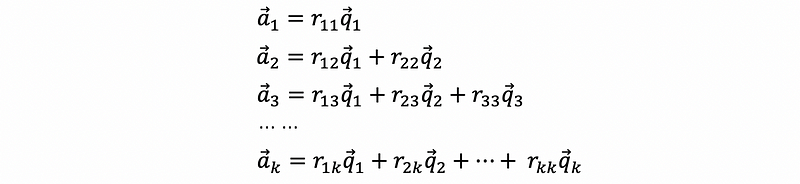
where r₁₁, r₁₂, … ∈ℝ. This equation is equivalent to,
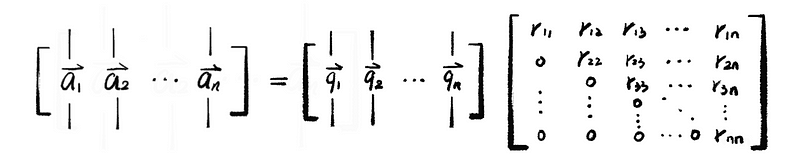
Suppose we have matrix Q and R defined by
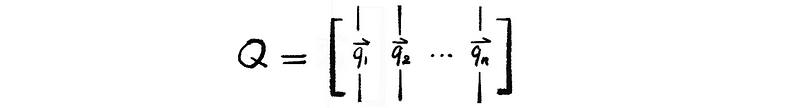

then we can write,
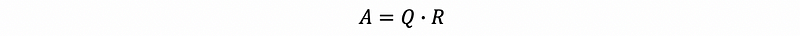
This is called the QR factorization of matrix A. Suppose A is an m × n matrix, then Q (orthonormal matrix) is an m × n matrix, R (upper matrix) is an n × n matrix.
(10) Calculate the Constant rij
So our problem is how we can calculate the R matrix? To understand the solution, remember we have,
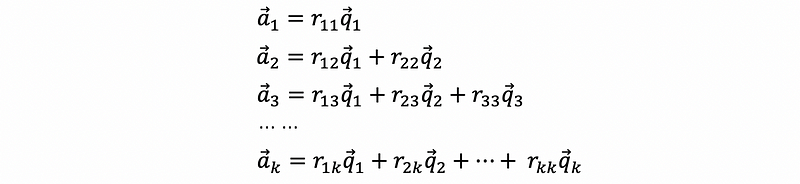
By the first line, if we multiply the q1 transpose (row vector) to both sides, we can have,
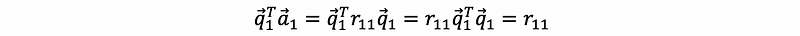
so, we can have,
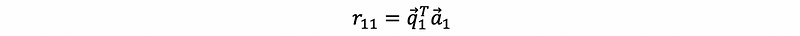
Continue to the second line, by multiplying the q1 transpose (row vector) to both sides, we can have,
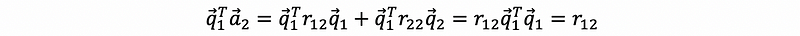
also, multiply the q2 transpose (row vector) to both sides, we can have,
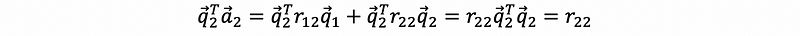
thus, we have,
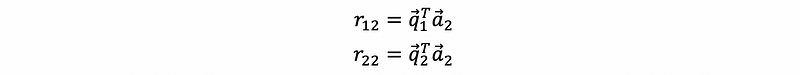
continue to the end, finally, we can have the generation expression of r, which is,
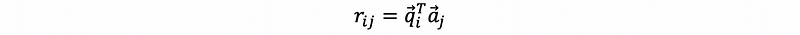
4. Gram-Schmidt Orthogonalization: An Example
Suppose we have a matrix A as
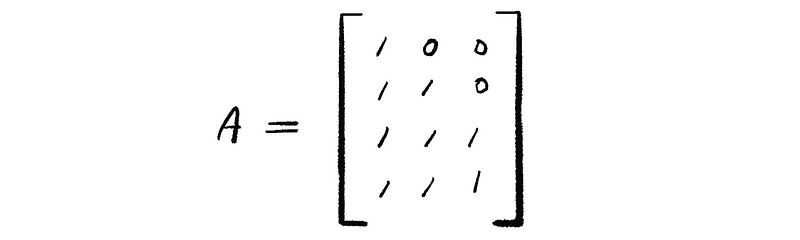
Apply the GS process to Col(A) and find a QR factorization.
Ans:
(a) Let’s first generate an orthogonal set of vectors,

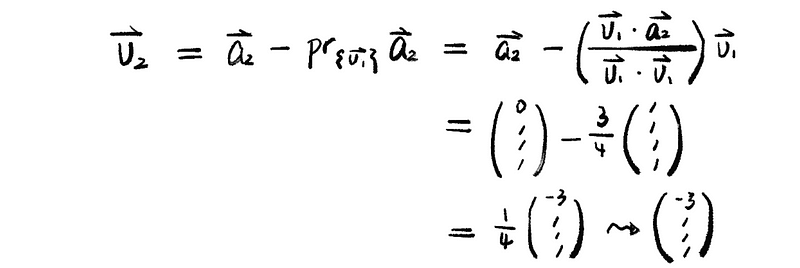
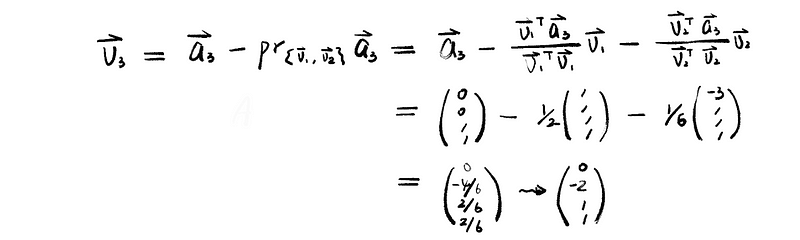
thus, we have the orthogonal matrix V as,
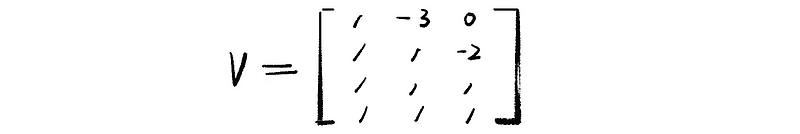
(b) Normalize V, then we can have an orthogonal matrix Q, which is,
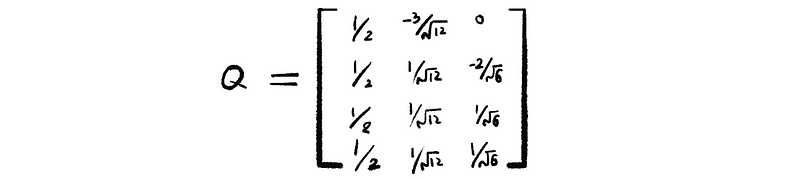
(c) Because we have,
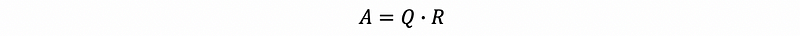
then we can have,
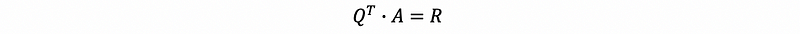
thus,
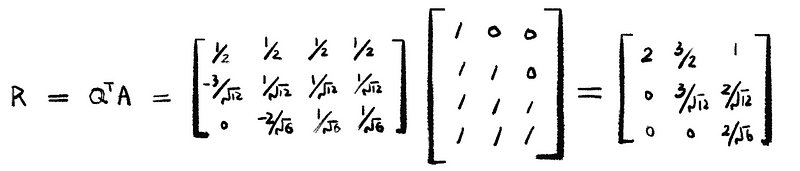
So finally, we find a QR factorization of the matrix A.