Linear Algebra 8 | Determinate, Computational Formula, 9 Properties of the Determinate,
Linear Algebra 8 | Determinate, Computational Formula, 9 Properties of the Determinate, Eigenvector and the Eigenvalue

- The First Definition of Determinate
(1) The First Definition of Determinate
Suppose A is an n × n square matrix, then det(A) is the function on the rows of a matrix that satisfies the following properties:
- Axiom #1: det(In) = 1
- Axiom #2: If you swap two rows of a matrix, then the determinate of this matrix will change signs
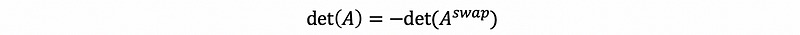
- Axiom #3: determinate is a function of each row with all other rows fixed.
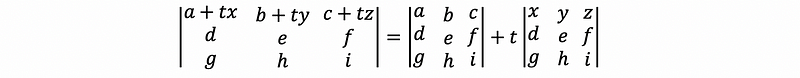
(2) Computational Formula
For any i-th row, j-th column entry aij of matrix A, we define an (n -1)× (n -1) matrix Mij, which is the matrix A removing its i-th row and j-th column. For example,

If we pick a row in A say row i, then,
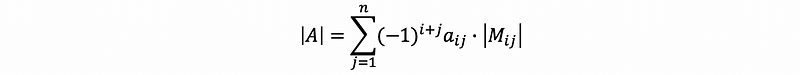
Also, if we pick a column in A say column j, then,
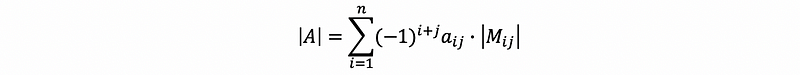
(3) Determinate And Singular Matrix
Remember we have proved in the part of the invertible matrix, that for a 2 × 2 matrix A that
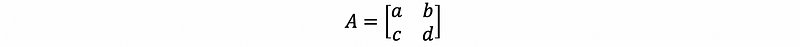
then if
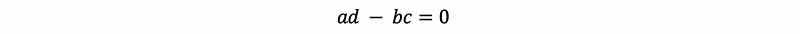
this matrix is singular.
Note that we can also have,
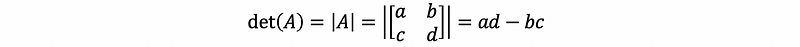
so if the determinate of matrix A equals zero, then this matrix is a singular matrix (non-invertible matrix). This conclusion can be applied to any n × n square matrix.
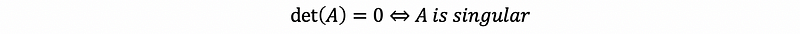
2. Properties of the Determinate
(1) Property #1 of the Determinate
If two rows of A are the same, then det(A) = 0.
Proof:
If two rows of A are the same, then if we swap these two rows, we can have the same matrix, that is,
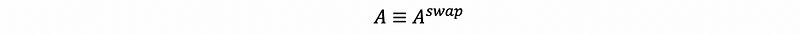
By Axiom #2, then we can have,
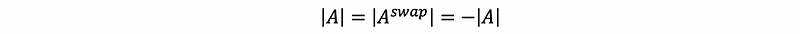
this is to say that,
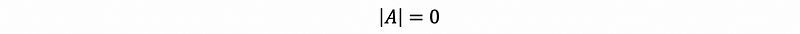
(2) Property #2 of the Determinate
If you have a row of zeros in A, then det(A) = 0.
Proof:
We start with the row of zeros and then take another row (whichever row is okay) and add it to the row of zeros. By this means, we create a matrix with two rows that are equal to each other. Thus, by property #1, we can know that det(A) = 0.
(3) Property #3 of the Determinate
If we add a multiply of one row to another row, then it leaves the determinate fixed.
Proof: For example, by Axiom #3, we have
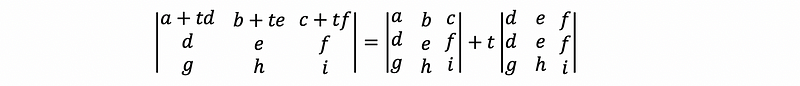
then by Property #1,
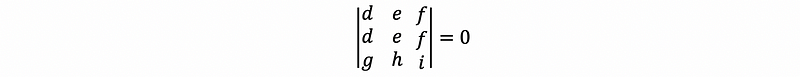
then, we can have,
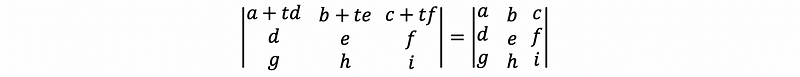
(4) Property #4 of the Determinate
Suppose we have a full-rank matrix A, then by row operations, we can have its reduced row echelon form as,

then, we can have,
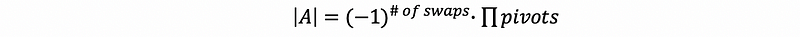
Proof:
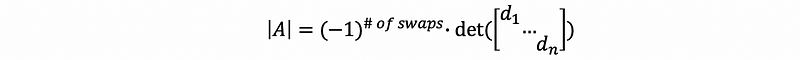
then,
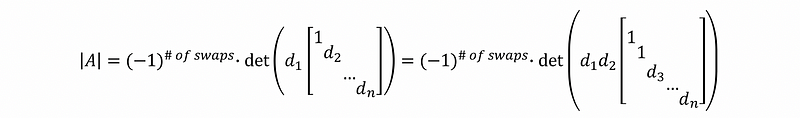
then …,
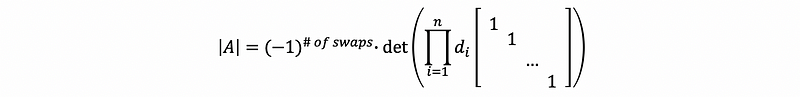
then,
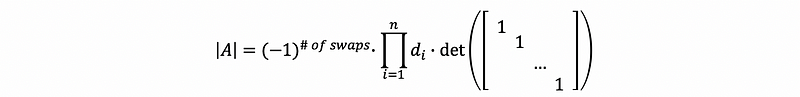
by Axiom #1,
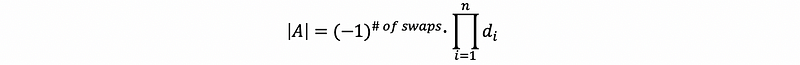
(5) Property #5 of the Determinate
Suppose we have an upper triangular matrix U, then its determinate det(U) equals the product of its pivots.
Proof:
This one is simple. During the process from REF to RREF, the values of the pivots remain the same, which means the result of property #4 holds for the upper triangular matrix (REF).
In general, we can also write this conclusion as,

where, by doing row reduction, the REF(A) = U.
(6) Property #6 of the Determinate
Suppose A and B are two upper triangular matrices, then the determinate of their product equals the product of all their pivots.
Proof:
The product of A and B is still an upper triangular matrix, and its pivots are the products of each of these corresponding pivots in A and B. Thus, by Property #5, we can get this conclusion.
(7) Property #7 of the Determinate
For any matrics A and B, we have,
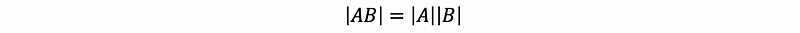
Proof:
By doing row reduction, we can change A to REF(A). Also, by doing row reduction, we can change B to REF(B).
By Axiom #3, we then have,
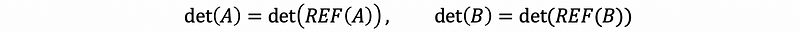
By property #6, we can then have,
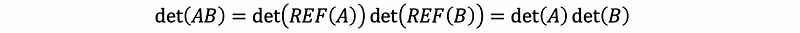
3. The Second Definition of Determinate
(1) The Second Definition of Determinate
If we define a function f that satisfies,
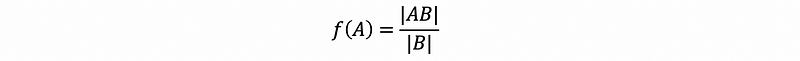
then, f is the determinate of A.
Proof:
By property #7, we can have,
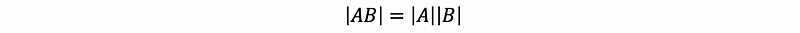
then,
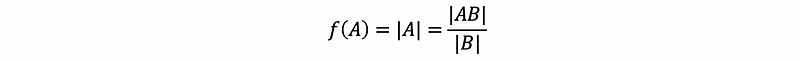
(2) Proof of the Three Axioms
- Axiom #1
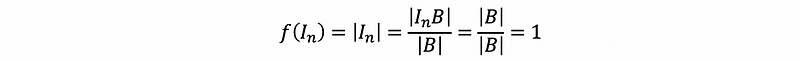
- Axiom #2
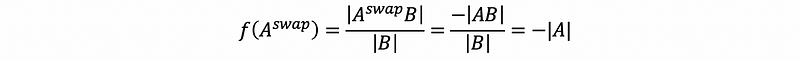
- Axiom #3: not proved here. Maybe to prove it sometime later.
(3) Property #8 of the Determinate
Suppose A is an invertible matrix, then,
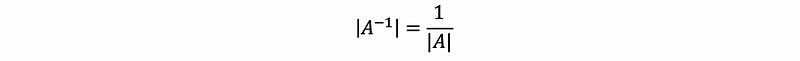
Proof:
By the second definition of determinate, we have,
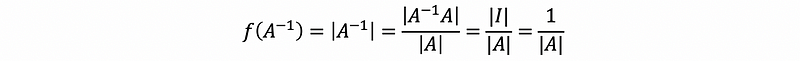
(4) Property #9 of the Determinate
For matrix A, we can have the determinate of its transpose equals the determinate of itself.
Proof:
Suppose we have the LU factorization of A, which is,
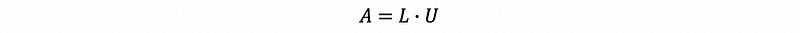
then we can have,
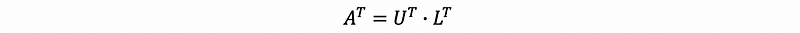
then,
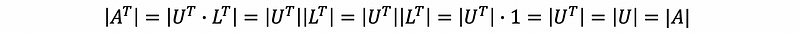
4. Determinate From a Geometrical View
Finally, remember this conclusion. The determinate of A is the positive or negative value of the volume of the parallelepiped determined by the row vectors of A. For example,
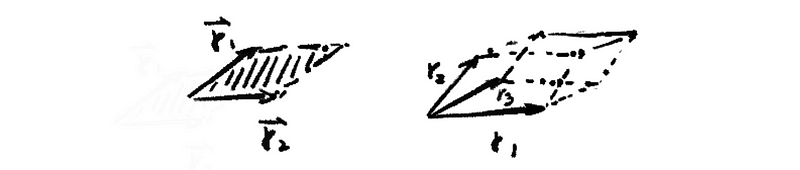
5. Spectral Theory
(1) The Definition of the Eigenvector and the Eigenvalue
Let matrix A be an n × n square matrix. Suppose we have a vector x ≠ 0. If there’s a constant λ satisfies,
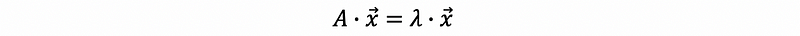
then x is an eigenvector for A corresponding to the eigenvalue λ.
Note that if x is an eigenvector for A then c · x must be an eigenvector for A.
Proof:

(2) Calculate the Eigenvector and the Eigenvalue
If we have,
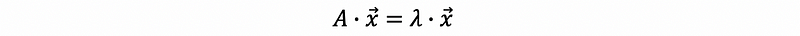
then,
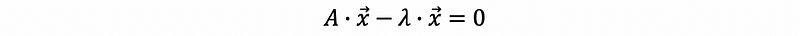
then,
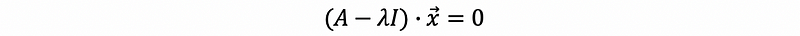
then x is in N(A-λI),
then A-λI is a singular matrix,
then the determinate of A-λI should be equal to 0, this is to say that,
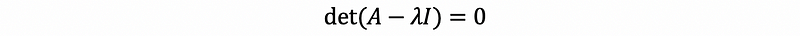
So that if we want to calculate the eigenvalue of A, we can construct the matrix A-λI and then assign its determinate to zero.