Linear Algebra 12 | Symmetric Matrix and Quadratic Forms
Linear Algebra 12 | Symmetric Matrix and Quadratic Forms

- Recall: The Spectral Theorem
In the definition of eigendecomposition above, we had the matrix Q as a matrix whose column space is the eigenspace of symmetric matrix A. What if we normalize this matrix Q and make it an orthonormal matrix? Suppose we have the set of all eigenvectors of A as {v1, v2, …, vn}, then if we define,
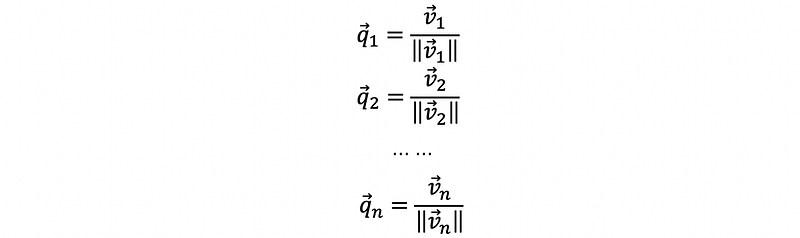
then we can construct matrix Q as
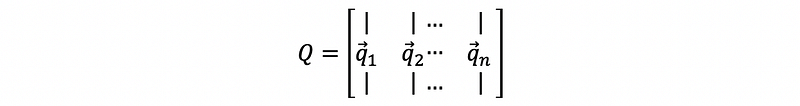
thus, we have,
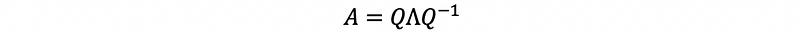
2. Symmetric Matrix
(1) The Definition of the Symmetric Matrix
Suppose we have a matrix A satisfies,
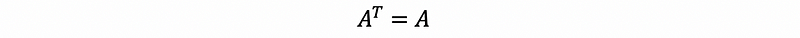
then, A is called a symmetric matrix.
(2) Proof of Spectral Theorem for Symmetric Matrix
To prove the spectral theorem for symmetric matrix, we have to prove that for any of the symmetric matrix, the symmetric matrix is diagonalizable and the eigenvector matrix S for the symmetric matrix is an orthogonal matrix.
- All eigenvectors of a symmetric matrix are orthogonal
Suppose we have eigenvectors v1, v2, …, vn corresponding to distinct eigenvalues of a symmetric matrix A, which satisfy,

then, for any vi and vj (i ≠ j), we have that,
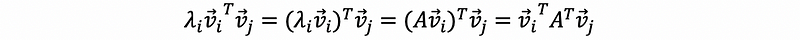
because we have the definition of the symmetric matrix as,
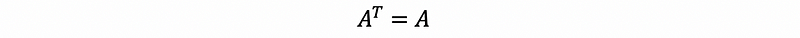
then,
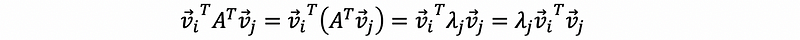
Because we have distinct eigenvalues, so that,
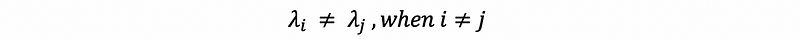
then we must have,
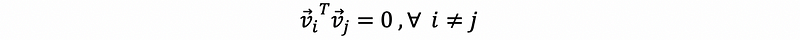
- Symmetric matrics are all diagonalizable
This proof can be a little bit tricky because we are going to use the mathematical induction for this proof.
It is clear that if A is a 1 × 1 symmetric matrix, then for eigendecomposition, the normalized eigenvector matrix U should be,
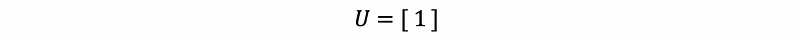
then we also have its diagonal matrix as,
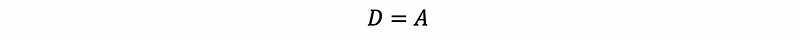
For the induction hypothesis, assume that every (n-1) × (n-1) real symmetric matrix A is diagonalizable.
Consider an n × n real symmetric matrix A. Let eigenvectors v1, v2, …, vn corresponding to distinct eigenvalues λ1, …, λn, then,

Normalize every eigenvector we can have,
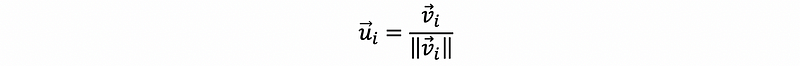
then, based on the fact that all the eigenvectors are orthogonal for a symmetric matrix,
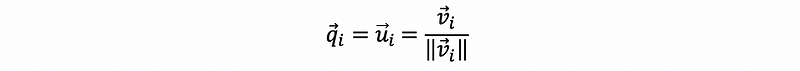
if we let,
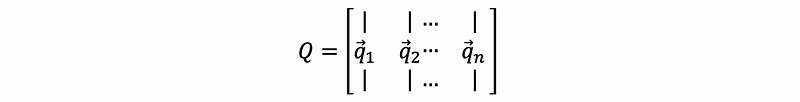
suppose we have,
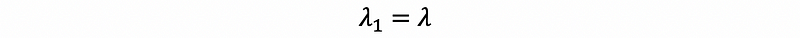
then,
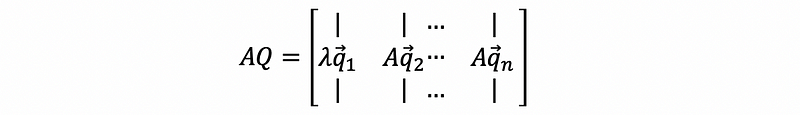
if we define some d satisfies,
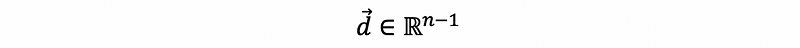
and,
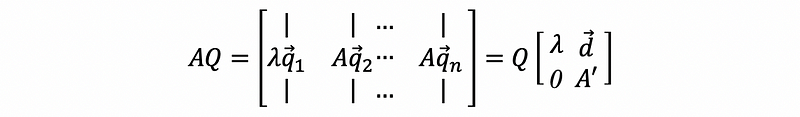
then based on the fact of the orthonormal matrix,
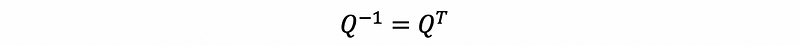
then,
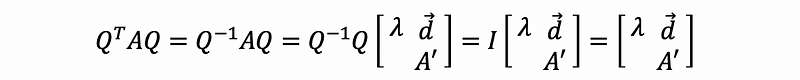
then we can have,

take transpose on both sides, we can then have,
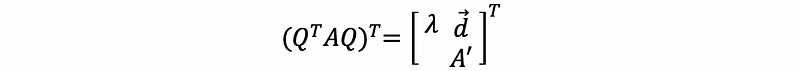
then,
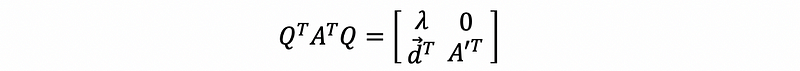
By the definition of the symmetric matrix,

then,
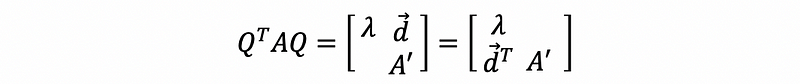
therefore,
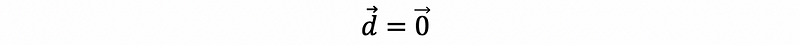
Hence,
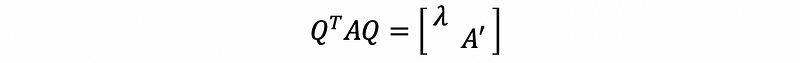
Based on the induction hypothesis, we have A’ is a diagonalizable symmetric matrix, so that,
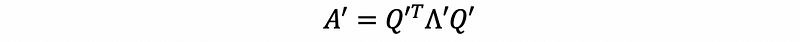
then,
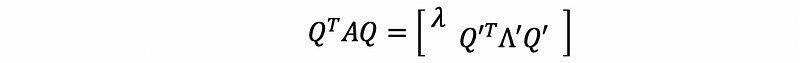
then,

then,
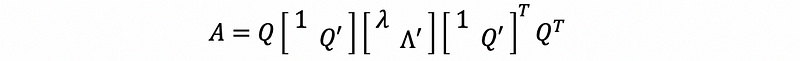
then,
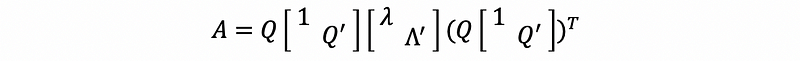
Let,
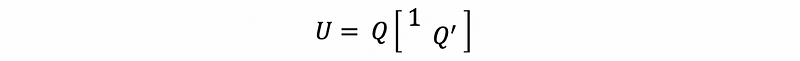
then,
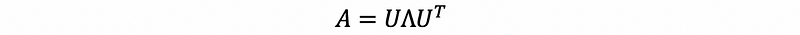
then we have to prove that U is an orthogonal matrix,
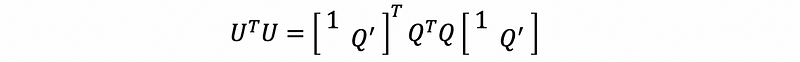
then because we have Q and Q’ are orthonormal matrics, so,

then,
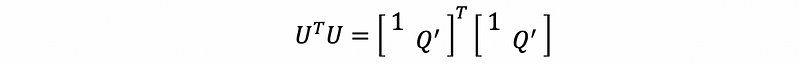
then,
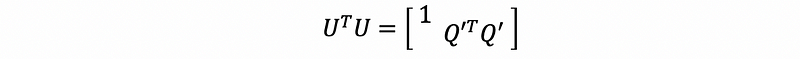
then,
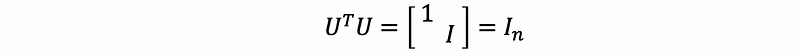
This is to say that symmetric matrics are all diagonalizable.
(3) Features of Symmetric Matrix
Based on the previous discussion, we can have the proposition that an n × n real symmetric matrix A is symmetric if and only if A is orthonormally (or orthogonally) diagonalizable.
- Fact #1: real eigenvalues
All eigenvalues of A are real.
- Fact #2: multiplicity equality
Given an eigenvalue λ of A, we can have its algebraic multiplicity equals its geometric multiplicity.
- Fact #3: orthogonal eigenvectors
Eigenvectors correspond to distinct eigenvalues are orthogonal.
(4) Eigendecomposition of Symmetric Matrix
Generally, when we talk about the eigendecomposition of a symmetric matrix, what we are generally talking about is,
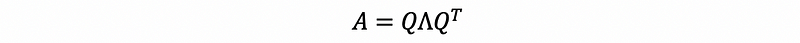
where Q is an orthonormal matrix and Λ is a diagonalized eigenvalue matrix. This is also to write,
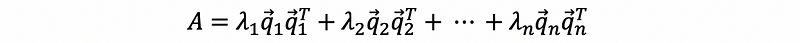
where the symmetric matrix A can be reckoned as a sum of rank 1 projections into each of the eigenvectors.
3. The Quadratic Form of a Symmetric Matrix
(1) The Definition of Quadratic Form
Let A become a symmetric matrix, define its quadratic form as,
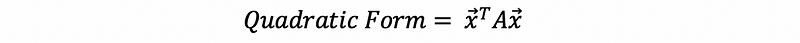
(2) The Meaning of the Quadratic Form of a Symmetric Matrix in the Projection Matrix Context
Let P be an m × n projection matrix that project any vector x to the column space of matrix B, so we can have the projected vector p as,
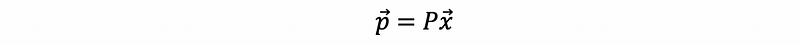
then the length of this projected vector p is,
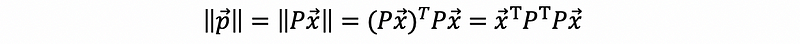
because P is an m × n matrix, then,
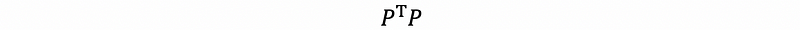
must be a n × n symmetric matrix. Suppose we assign that,
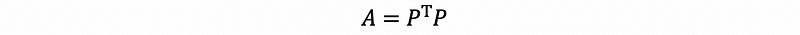
then,
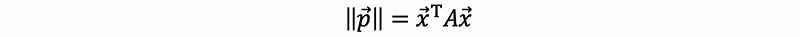
So basically, the meaning of this quadratic form the length of any projected vector onto the column space of B.
(3) Solving the Symmetric Matrix of a Quadratic Form
Suppose we have a quadratic form which is,
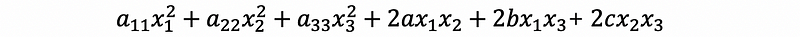
then, we can write it to the symmetric matrix form,
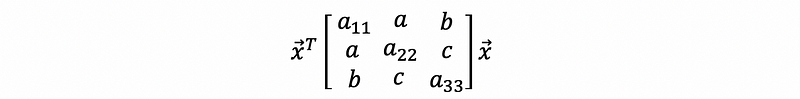
(4) Find the Projected Vector that Has the Largest Length
Because we can project any vector onto the column space of B by the projection matrix P, then it is okay for us to calculate any possible length of a projected vector p.
This question will be meaningful if we restrict the length of any vector x (to be projected) to 1. And by doing so, we can then calculate the longest possible length of this vector x projected onto the column space of B. This is to say,

For example, suppose we have a matrix B as,
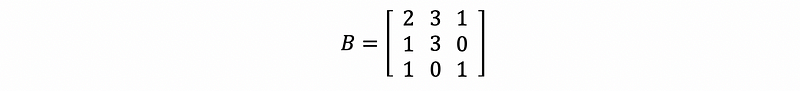
The LU-decomposition of B is,
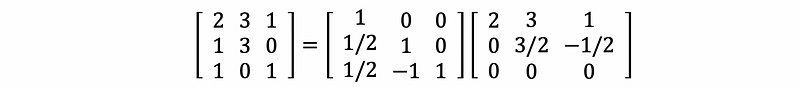
Then the column space of B is,
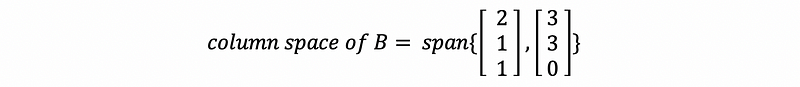
Therefore, we can have the column space as a plane (x-y=z if calculated),
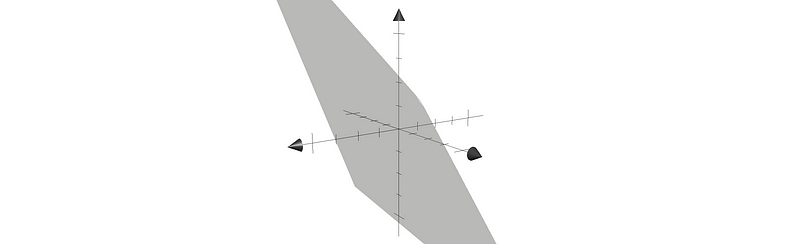
Then, its projection matrix P is,
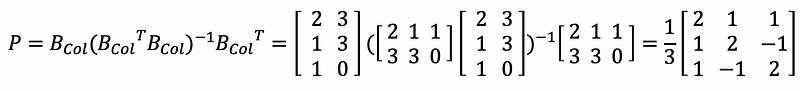
It is clear to know that P is a symmetric matrix, and we have the fact that,
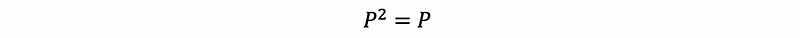
then,
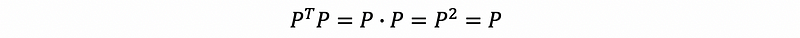
So the symmetric matrix in the quadratic form is supposed to be,
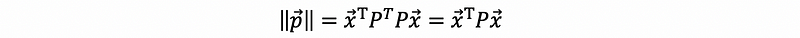
suppose we want to find the longest p in the space, then we are supposed to have,

We can easily find out that when x is in the column space of B, we can have the longest p in the space, which equals to 1. When we have x in the column space of B, then,
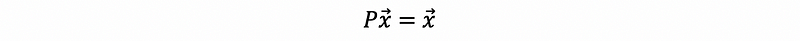
So it’s quite clear that x is the eigenvector of P corresponding to the eigenvalue λ = 1. And also we have that,
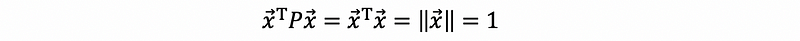
Therefore, if the symmetric matrix in the quadratic form is a projection matrix, then the unit vector x that has the longest projected vector p is suppose the unit (normalized) eigenvector corresponding to the eigenvalue of λ = 1.
(5) The Eigenvalues of A Projection Matrix
We have covered that all the projection matrics are symmetric. However, the symmetric matrics are not always the projection matrics. The difference is that the projection matrics are a kind of symmetric matrics that must have only 0 and 1 eigenvalues.
Proof:
Suppose P is a projection matrix, and x is the eigenvector corresponding to the eigenvalue λ, then,
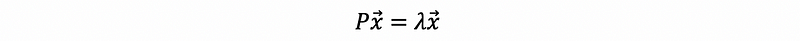
there is also that,
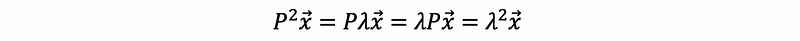
Based on the fact that,
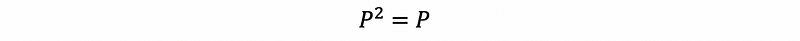
then,
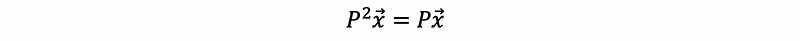
then,
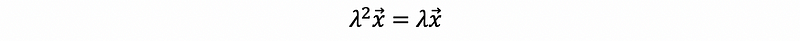
then,
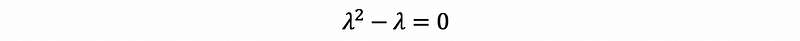
solve by,

(6) Loose Condition: Find the Projected Vector that Has the Largest Length (the symmetric A is not supposed to be a projection matrix)
If we want to focus on a more general case that is to have,
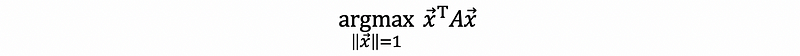
Since the symmetric matrix A is orthonormally diagonalizable, then we can eigendecomposite A as,
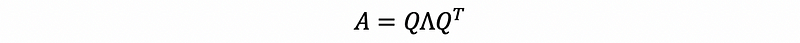
then,

if we define that,
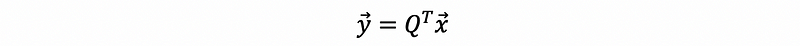
then,
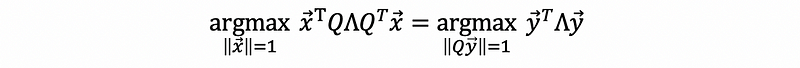
this is equivalent to (Q only change the direction, not the length),
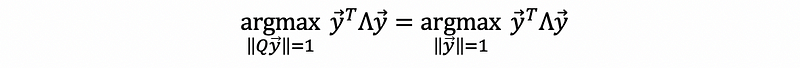
Now we have that,
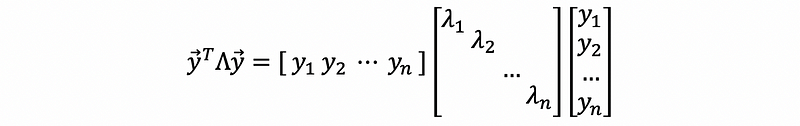
then,
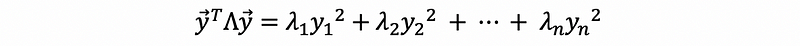
Assume that we have the relationships of the eigenvalues as
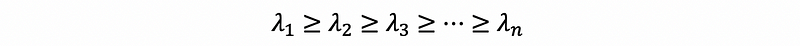
then,
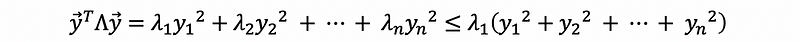
because we have,
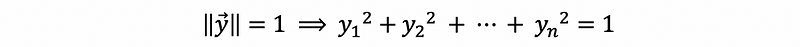
then,
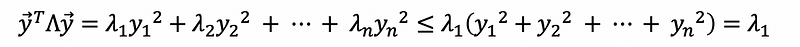
where λ1 is the largest eigenvalue of the symmetric matrix A.
Based on this inequation, we can see the maximum value is achieved if and only if y1=1 and y2 = y3 = … = yn = 0. Thus, we have,
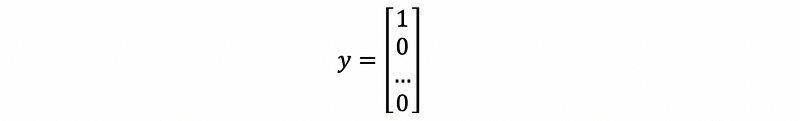
then, because of the condition that,
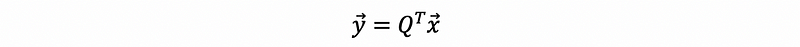
then,
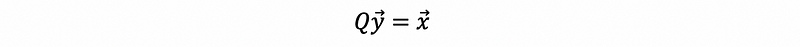
then,
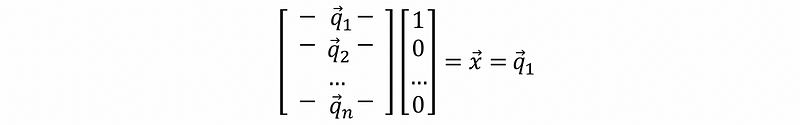
Then we can reach the conclusion that the quadratic form,
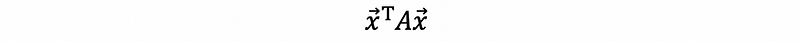
achieves its maximum value λ in th direction of the eigenvector corresponding to the max eigenvalue λ. This is to say that,
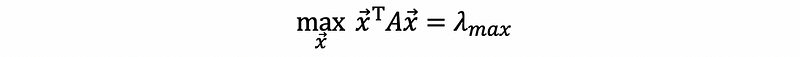
and,
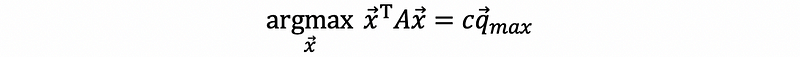
where qmax is the eigenvector corresponding to the max eigenvalue λmax.
(7) The Definition of Positive Definite Quadratic Form
Suppose for a quadratic form where A is a symmetric matrix,
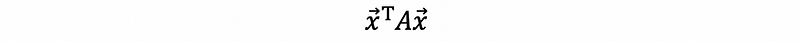
if all eigenvalues of A are positive, then this quadratic form is called positive definite.
(7) The Definition of Semi-Definite Quadratic Form
Suppose for a quadratic form where A is a symmetric matrix,
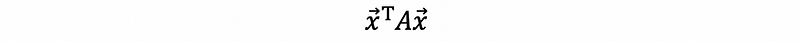
if all eigenvalues of A are non-negative, then this quadratic form is called positive definite. For a quadratic form of the form,
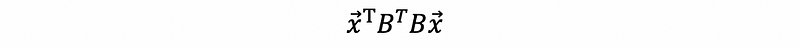
this is always a semi-definite quadratic form.
Proof:
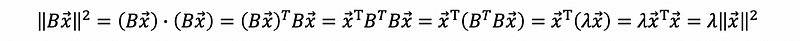
Because we have that,

then,
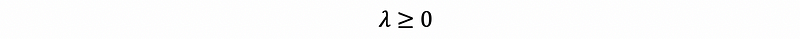
(7) The Definition of Indefinite Quadratic Form
Suppose for a quadratic form where A is a symmetric matrix,
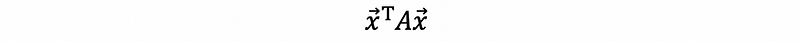
if eigenvalues of A are mixed with both negative values and positive values, then this quadratic form is called positive definite.