Linear Algebra 14 | Gershgorin Circle Theorem, Householder’s Reflection, QR Algorithm, and…
Linear Algebra 14 | Gershgorin Circle Theorem, Householder’s Reflection, QR Algorithm, and Condition Number

- Gershgorin’s Disk Method
(1) The Definition of the Radius
Suppose we have a matrix A defined as

If we define Ri equals the sum of the absolute values of the entries in the i-th row expect the ii-th entry. This is to say that,
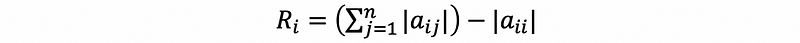
(2) Gershgorin Circle Theorem
If we take the disks in ℂ of the radius Ri centered at aii, then the eigenvalues of A are inside these disks. To express this, we have,
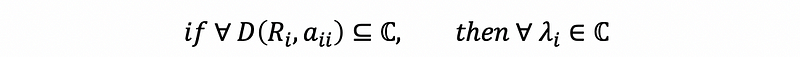
Proof:
Suppose we have,
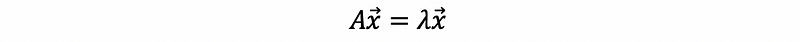
If we write,
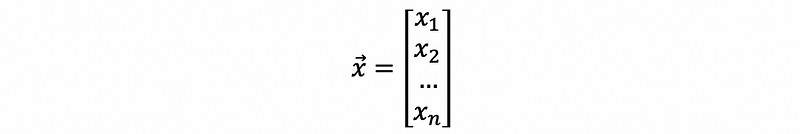
For x1, x2, …, xn, we pick a xi satisfies,
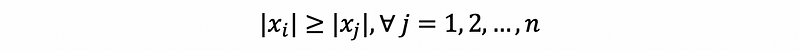
then look at the i-th row of A, we can have that,
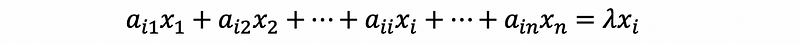
so,
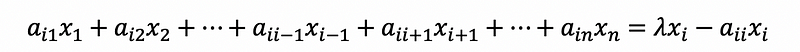
then,
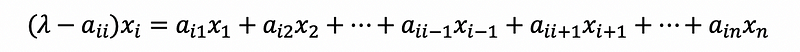
Take the absolute values,
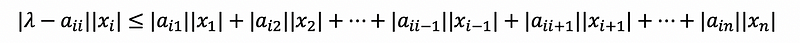
then, divided |xi| to both sides,

Because
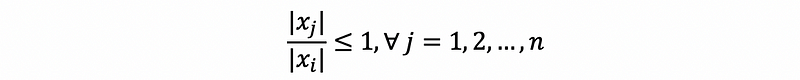
then,
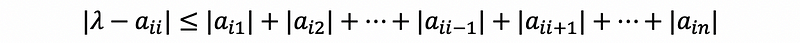
By the definition of the radius,
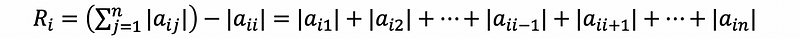
then,
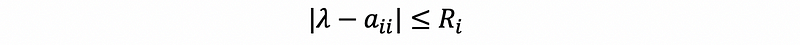
This means that,
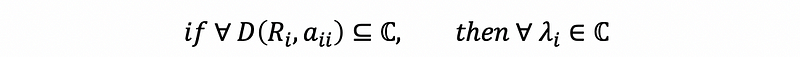
(3) Fact #1 of Gershgorin Circle Theorem: Diagonalizable
If the disks are disjoint, then A is diagonalizable.
Proof:
Because a matrix is diagonalizable if and only if for each eigenvalue the dimension of the eigenspace (geometric multiplicity) is equal to the algebraic multiplicity of the eigenvalue.
When the disks are disjoint, that means for all the eigenvectors, we have its geometric multiplicity equals its algebraic multiplicity (=1), which is basically the same definition of a diagonalizable matrix.
(3) Fact #2 of Gershgorin Circle Theorem: Invertible
If disks are all away from zero, then A is invertible.
Proof:
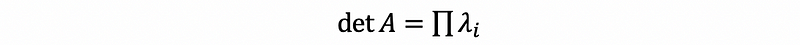
Because disks are all away from zero,
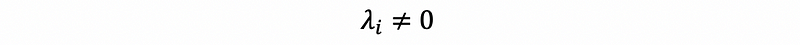
therefore,
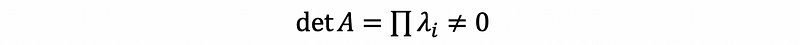
So A is an invertible matrix.
2. Householder’s Reflection
(1) Recall: QR Factorization by Gram-Schmidt Orthogonalization
The G-S process to orthogonalize the a ’s is:
- Normalize a1

- Find q2 by a1
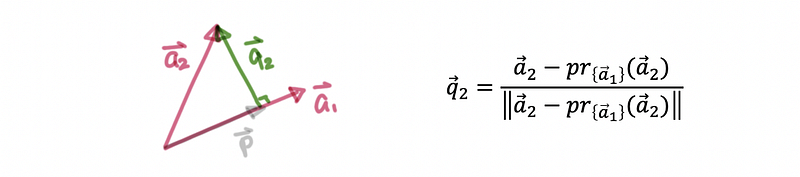
Because q1 = c · a1, then we can have,
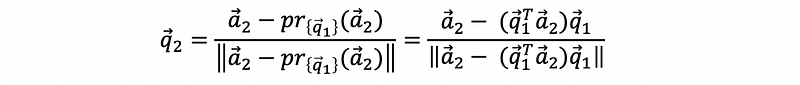
- Continue, find q3 by a1, a2
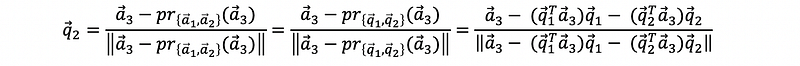
- Continue … until we find the set {q1, q2, …, qn}
By the above discussion, we can find out that we construct a set {q1, q2, …, qn} satisfies,
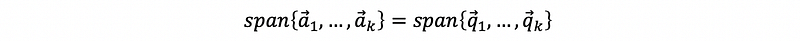
so we can rewrite each the vector ai in the form of the linear combination of {q1, q2, …, qn}, which is,
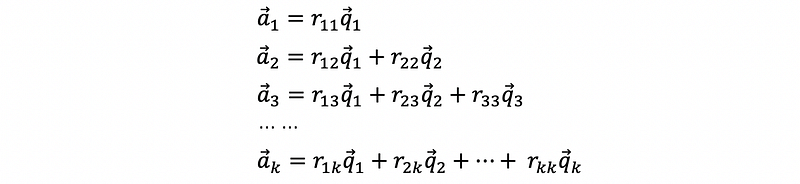
where r₁₁, r₁₂, … ∈ℝ. This equation is equivalent to,
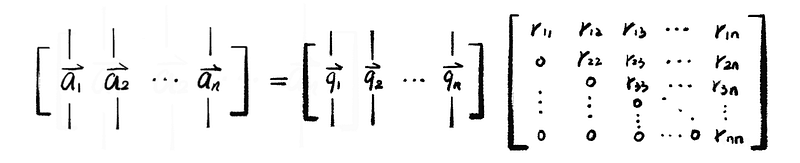
Suppose we have matrix Q and R defined by
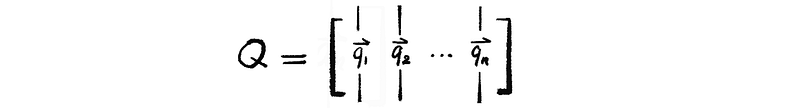

then we can write,
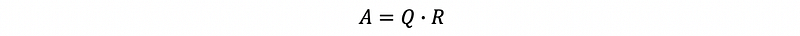
This is called the QR factorization of matrix A. Suppose A is an m × n matrix, then Q (orthonormal matrix) is an m × n matrix, R (upper matrix) is an n × n matrix.
How we can calculate the R matrix? If we multiply the q1 transpose (row vector) to both sides, we can have,
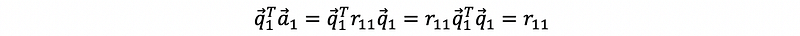
so, we can have,
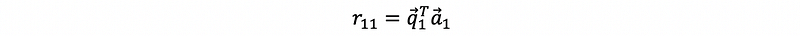
Continue to the second line, by multiplying the q1 transpose (row vector) to both sides, we can have,
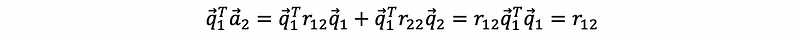
also, multiply the q2 transpose (row vector) to both sides, we can have,
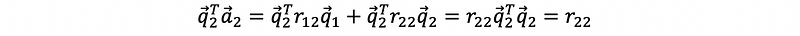
thus, we have,
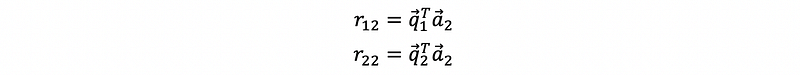
continue to the end, finally, we can have the generation expression of r, which is,
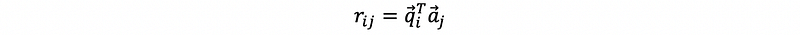
(2) Householder’s Reflection
Suppose we have a vector v.

The transformation Q takes v to,
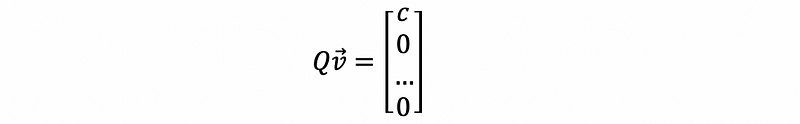
Because Q is an orthonormal matrix, so the length of the Qv should be equal to the length of the vector v. Thus, we have,
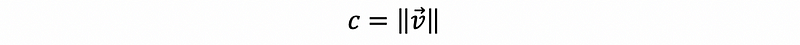
Suppose we have a unit vector z satisfies,
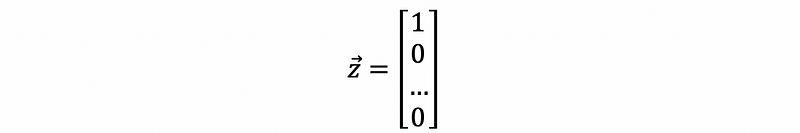
Then how can we find a matrix H that transforms v into the linear combination of the vector z? The answer is tricky because we have to construct an auxiliary vector w (literally).
Knowing that what we would like to to get finally is Qv, which can be constructed by c times z.
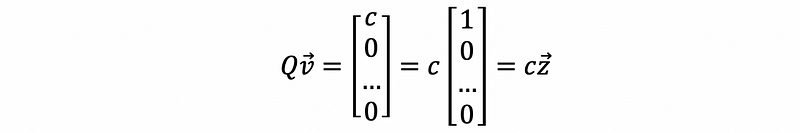
Then, we construct w by.

Therefore, we have,

Based on this graph, we have,
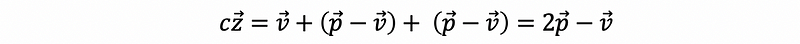
Because p is the vector v reflected through line determined by w, then, we have,
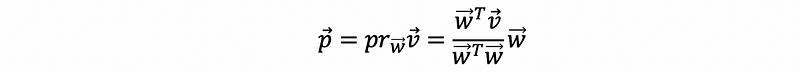
then,
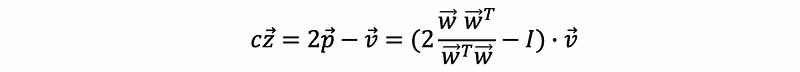
Suppose we have,
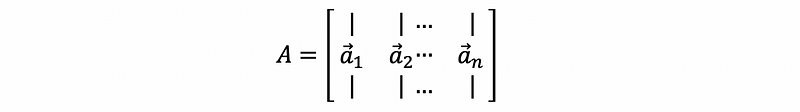
then,
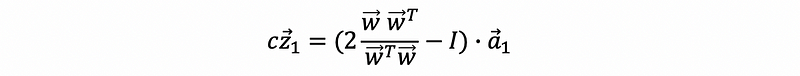
If we let,
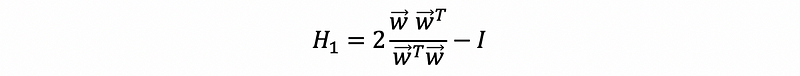
where,
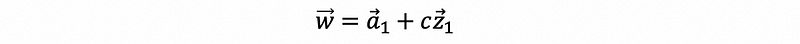
then,

by,
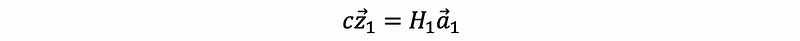
then,
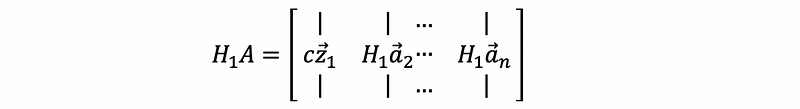
This is also to say that ( * = non-zero entry ),

We select the lower right part of this matrix A’, this is to have that,

We can also find a Householder transformation matrix H’ of this matrix A’, which is,

We use this H’ to construct H2, which is,
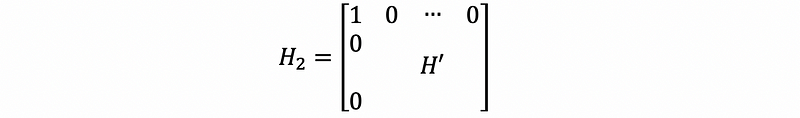
then, we can have,

Contiue this process until we get an upper triangular-ish matrix,
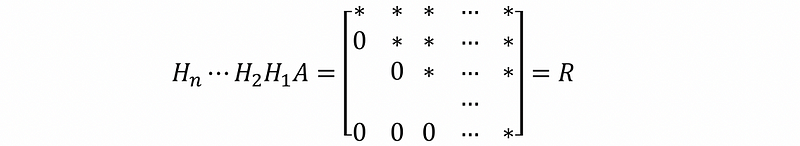
Thus,
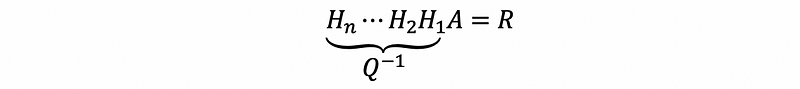
So,
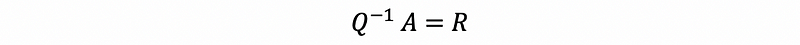
then,
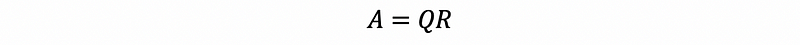
3. QR Algorithm
QR algorithm is a quick way to find the eigenvalues.
(1) A Fact of QR Factorization
Because we have known that, by Householder or GS Orthogonalization, we can have that,
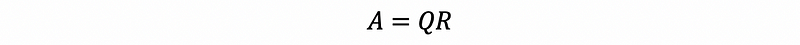
Then we are able to say that the matrix RQ is similar to matrix A.
Proof:
Suppose we have A’ satisfies,
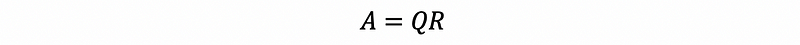
then,
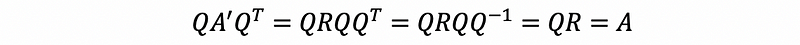
then we are able to say that,
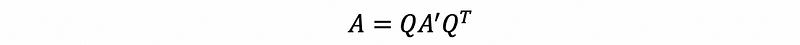
therefore, by definition, we have,
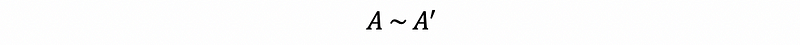
(2) Steps of QR Algorithm
- Calculate A = QR, get the matrix Q and R by Householder or GS Orthogonalization.
- Construct A1 by,
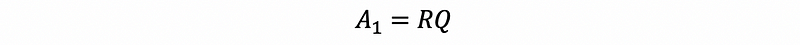
Because A1 is similar to A, then the eigenvalues of A1 is equal to the eigenvalues of A.
- Do QR factorization to A1, then,
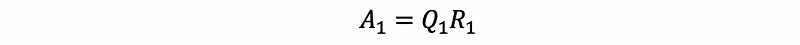
- Construct A2 by,

- Do QR factorization to A2, then,
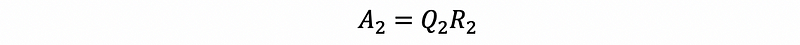
- Construct A3 by,
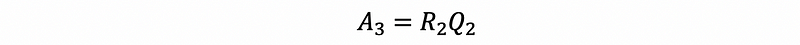
- …..
- Continue this process, until we find an An that is an upper triangular matrix with eigenvalues on its diagonal.
Note that this algorithm is because the result of this process is almost always converge.
(3) The Definition of the Hessenberg Matrix (aka. Upper Hessenberg Matrix)
Suppose we have an n × n matrix A satisfies hij = 0 for all i > j+1, then this matrix is called a Hessenberg Matrix.

(4) Preprocess of the QR Algorithm
We can use a tricky way to make the QR algorithm converges rapidly. This way is to write A into its Hessenberg form.
First of all, we have to work out the householder matrix H of the matrix A by,
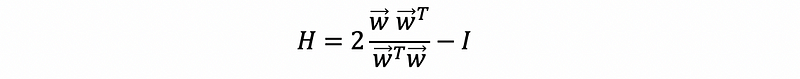
where,
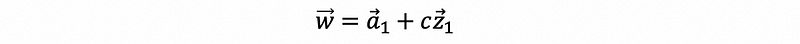
Then the Hessenberg form of A is,
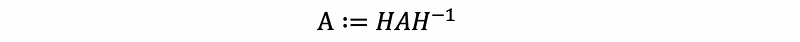
The reason why we can use this is the Hessenberg form of A is similar to A.
Proof:
Because,
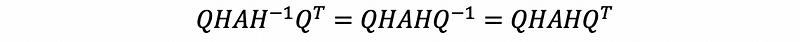
therefore,

4. Condition Number
(1) Relative Change Problem
Consider a system of equations,
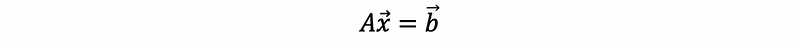
Suppose we introduce a small change in b, then what is the resulting change in x?
To think about:
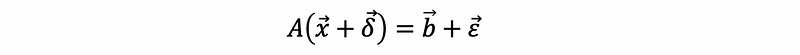
Then,
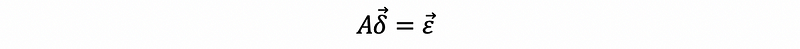
But this is still unclear how much the change is. Thus, we have to construct a ratio.
(2) Upper Bound of the Changing Ratio
Suppose we define the relative changing ratio r as,
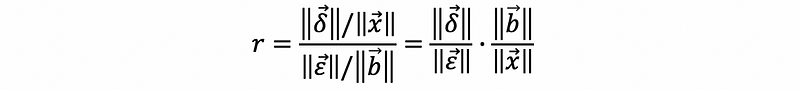
Suppose A is a diagonal matrix and λ1, λ2, …, λn are eigenvalues of A, then,
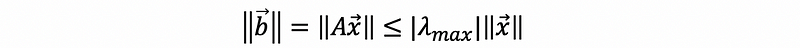
so,
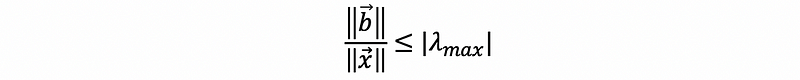
Also,

so,
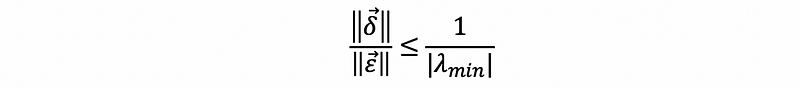
therefore,
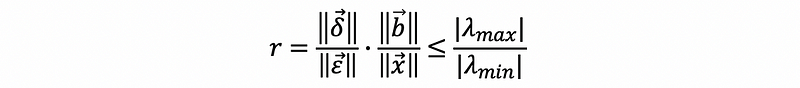
This is the upper bound of the changing ratio.
By this ratio, we can then know when,
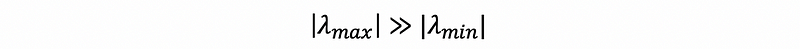
we will have,

(3) Recall: Norm of a Vector
Suppose we have a vector v satisfies,

then the norm of this vector is,

(4) The Definition of the Norm of a Matrix (aka. Induced Norm)
Suppose we have a matrix A, then the induced norm (norm) of A is defined by,
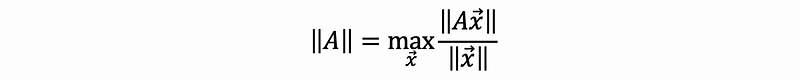
We can denote the induced norm of A by,
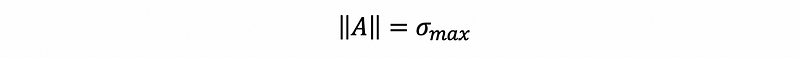
This is also,
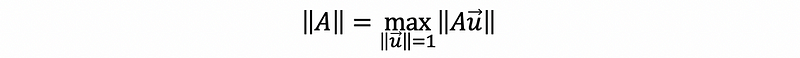
Proof:
Because,
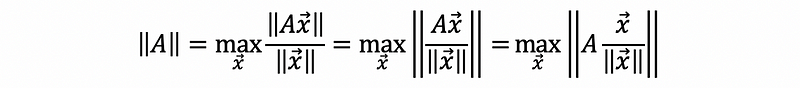
If we define,
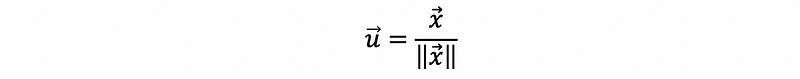
then,
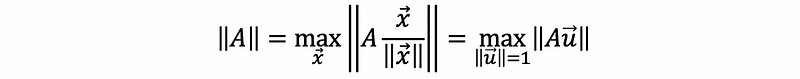
(5) The Definition of the Condition Number of a Matrix
Suppose we have a matrix A, then the condition number of this matrix A is its norm multiplying the norm of its inverse. This is to say that,
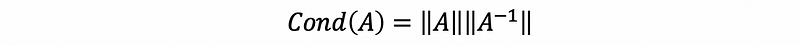
By definition of the induced norm,
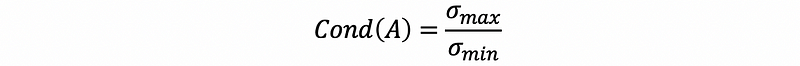
This is also the eccentricity of the ellipse.