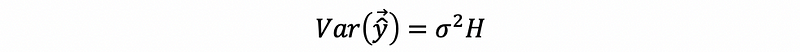Linear Regression 5 | MLR, Hat Matrix, and MLR-OLS Evaluation
Linear Regression 5 | MLR, Hat Matrix, and MLR-OLS Evaluation

- Multiple Linear Regression
(1) Recall: Simple Linear Regression Model
The form of the simple linear regression for a given sample of two variables x and y (or a dataset of two variables) is,
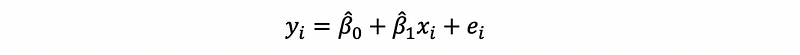
What if we have more than two variables for a linear model?
(2) The Definition of Multiple Linear Regression
Suppose we have p variables, and x1 to xp-1 are our independent variables and y is our dependent variable, then, the formula can be written as,
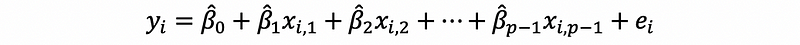
this is also,
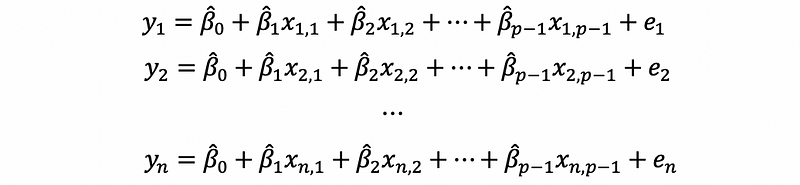
Because this is a linear equation system, we can also rewrite this as the form of matrix production.
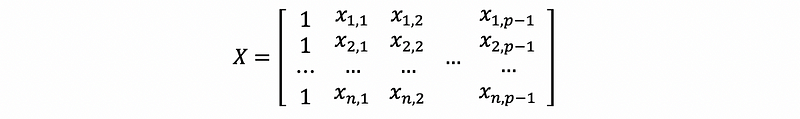
And,
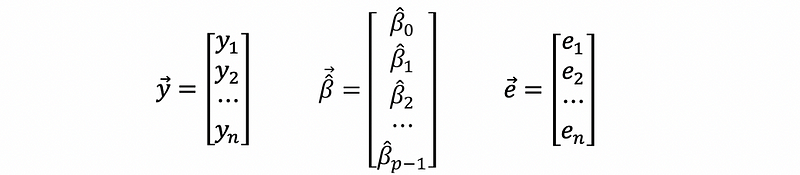
thus, we have,
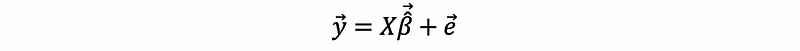
(3) Strong Assumption of Multiple Linear Regression
Similarly to the simple linear regression, we are able to say, for the real model,
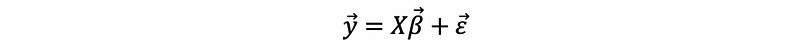
the error term should follow,
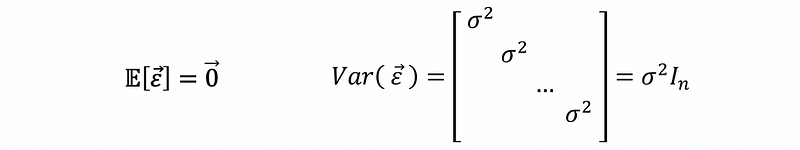
Suppose we denote multivariate normal distribution as MN, then the strong assumption can be written as,
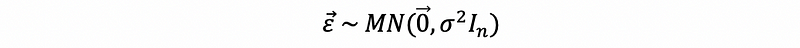
(4) OLS: Sum of Squared Residuals
Recall in the SLR, we have defined that,
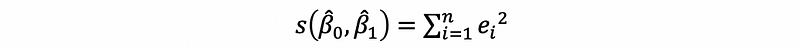
Similarly, we define that,

then, to solve OLS estimators, our goal is to optimize the following problem,
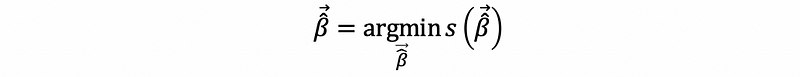
(5) Projection Matrix and OLS for Multiple Linear Regression
Recall what we have talked about for the projection matrix,
Series: Linear Algebrmedium.com
Now let’s define the projection of vector y onto the column space of matrix X as,
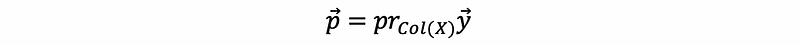
Based on the fact of the matrix projection,
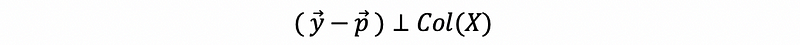
then,
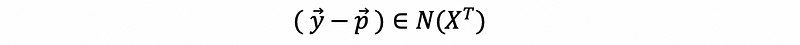
This is equivalent to,
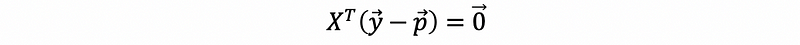
Then, the optimize problem is equivalent to solve when,

this is to say that,
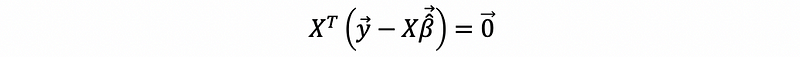
then,
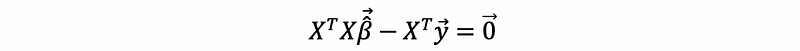
then,

then,
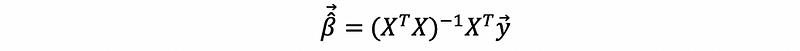
We can also solve this result by matrix differentiation, but because we didn’t introduce this in our sections, it is not the most preferred proof in this case.
2. Hat Matrix
(1) Hat Matrix for MLR
The hat matrix in regression is just another name for the projection matrix. For a given model with independent variables and a dependent variable, the hat matrix is the projection matrix to project vector y onto the column space of X.
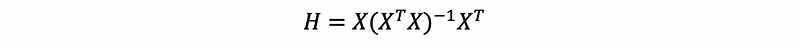
(2) Properties of the Hat Matrix
Because the hat matrix is a projection matrix, so it has all the features of the projection matrix,
- Property #1: Symmetric
Because the hat matrix is a specific kind of projection matrix, then it should be a symmetric matrix.
Proof:
For any square and invertable matrix A, the inverse and transpose operator commute,
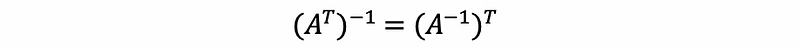
Then, we have,
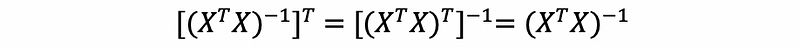
So, X^TX is a symmetric matrix. Then,
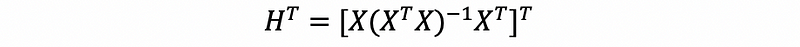
then,
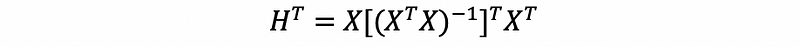
then,
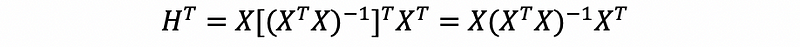
then,
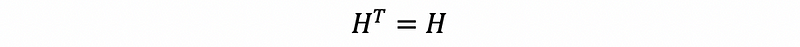
- Property #2: Idempotent
Because the definition of a project matrix is to project a vector onto the column space of another matrix, then it will be idempotent.
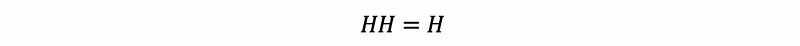
(3) Fitted Value
Based on our conclusion of the OLS estimator, we can then have the fitted value as,
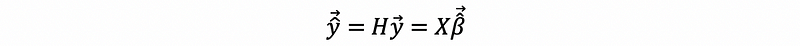
(4) The Residual of the OLS
The difference of the observed values and the fitted values is called the residual,
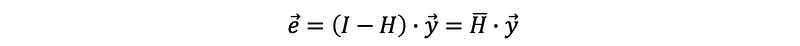
Proof:
By definition,
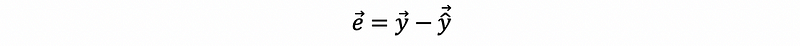
then, based on the result of the fitted value for MLR,
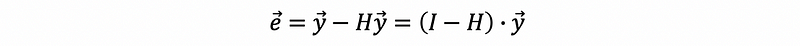
Suppose we define that,
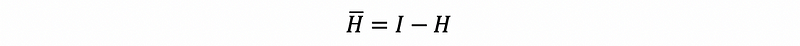
then,
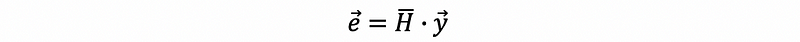
Note that because H-bar matrix is derived from the hat matrix, so it has some of the properties that the hat matrix has. For example,
- Property #1: Symmetric
- Property #2: Idempotent
For matrix H-bar, we also have,
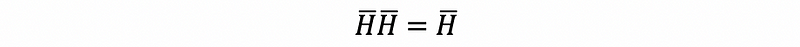
Proof:
By definition,
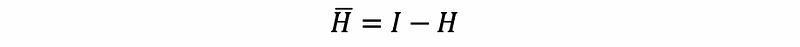
then,
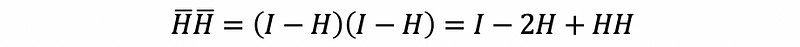
By the fact that,
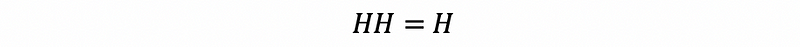
then,
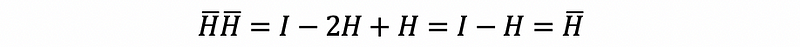
Note that this H-bar matrix is one of the most important matrix for MLR.
3. OLS Evaluation
(1) Evaluation on OLS for Multiple Linear Regression
Similarly, the OLS estimator for MLR is also the best linear unbiased estimatior (BLUE).
Proof:
For linearity, we can write,
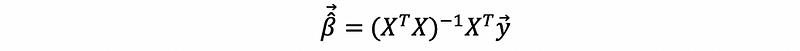
this shows a linear relationship between the OLS estimator and the vector y.
For the bias of the OLS estimator, by its definition,
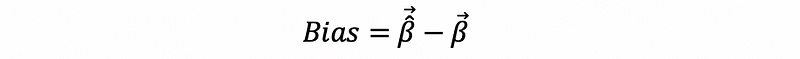
then,
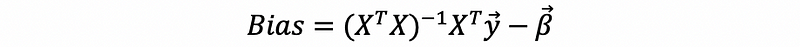
Because,
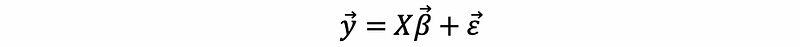
then,
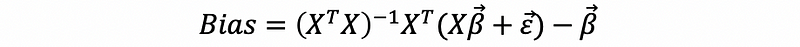
then,
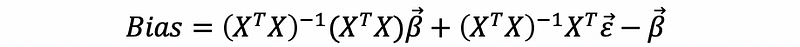
then,
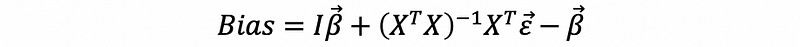
then,
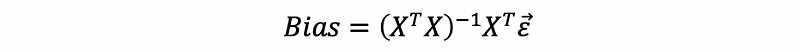
then,
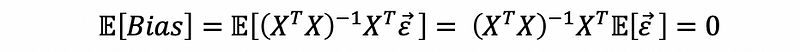
(2) Expectation of the OLS Estimators
Based on the fact that the OLS estimator is unbiased, then we can have,
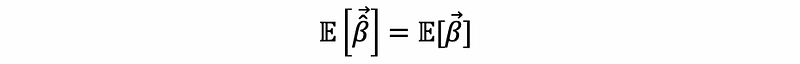
(3) The Definition of the Variance-Covariance Matrix
To calculate a variance of a vector of random variables, we are going to have a variance-covariance matrix. Suppose we have a vector of random variables x1, x2, …, xn,
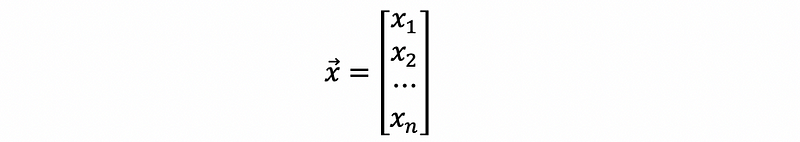
then, the variance of this vector is defined by,
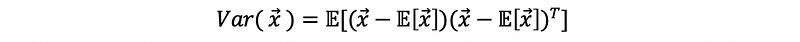
then,
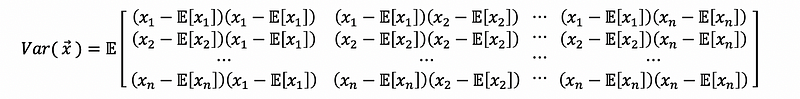
this is also,

and this is also,
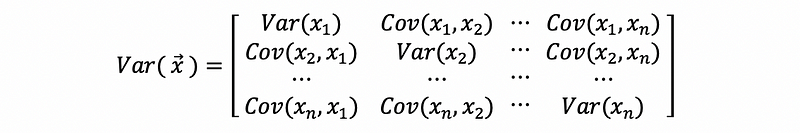
(4) Variance-Covariance Matrix of the OLS Estimators
In the sections of SLR, when we calculate the variance of an estimator, we are then going to have a single value of the variance. But, however, because the OLS estimator for MLR is a vector, then to calculate its variance, we are going to have a variance-covariance matrix.

Proof:
By the definition of the variance-covariance matrix, we are then going to have,
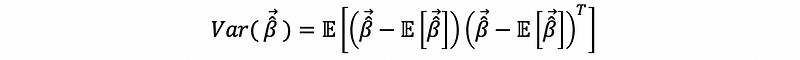
By the expectation of the OLS estimator,
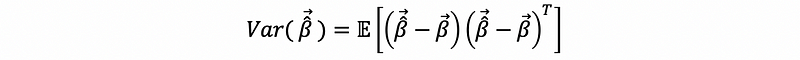
then, by the bias (estimated error) of the OLS estimator,
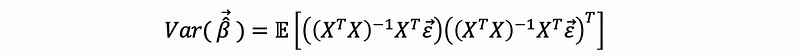
then,
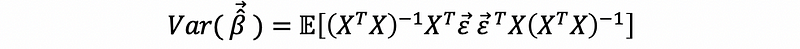
then, because X is fixed in this case,

by definition of the variance-covariance matrix,
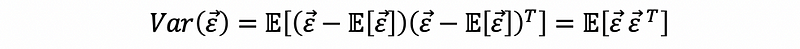
By our assumption,
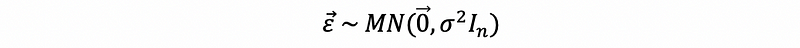
then,
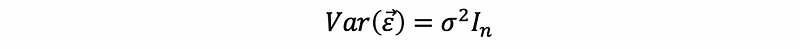
then,
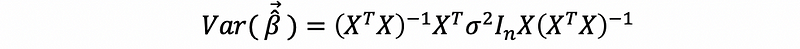
then,
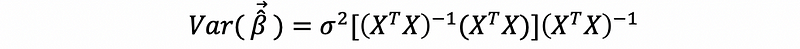
then,

(5) Expectation of the Fitted Value
Because X is fixed in this case, then, by the unbiasness of the OLS estimator,
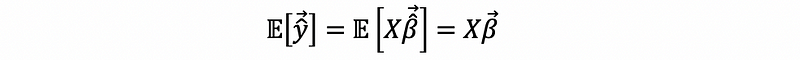
(6) Variance of the Fitted Value
The variance-covariance matrix of the fitted value is,
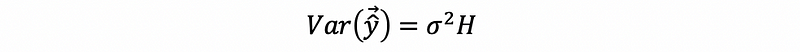
Proof:
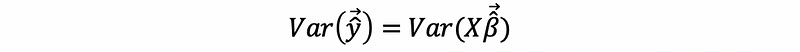
then,
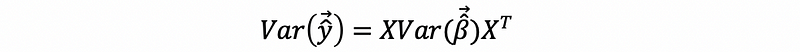
by the variance of the OLS estimator,
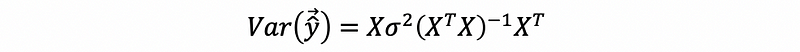
then,
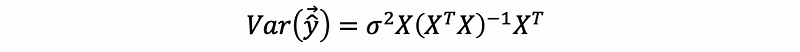
by the definition of the hat matrix,