Probability and Statistics 4 | Expectation, Variance, Moment, and Features of Common Distributions
Probability and Statistics 4 | Expectation, Variance, Moment, and Features of Common Distributions
- Expectation
(1) The Definition of Expectation
If X is a discrete random variable, we define the expectation (or expected value) of X by, (which is similar to calculate means and averages)

Note that we call the quantity 𝔼[X] the first moment of random variable X.
(2) Expectation: An Example
Suppose that X is a random variable such that,


So the expectation of random variable X is,

(3) The Definition of Bernoulli Distribution
A random variable X is said to be Bernoulli if it has a PMF such that,

Then, we will write X ~ Ber(p). If X ~ Ber(p), then 𝔼[X] = p.
Proof:

(4) The Properties of Expectation
- Fact #1

Because of this fact, we can conclude that 𝔼 is a linear operation.
- Fact #2

- Fact #3

(5) Does Expectation Fully Characterize a Random Variable?
The answer is no. Even if we have 𝔼[X] = 𝔼[Y], X and Y are not the same random variables. For example, in the graph below, even we have 𝔼[X] = 𝔼[Y], the random variable X and Y do not obey the same distribution. For random variable Y, the data is very spread out, while for random variable X, the data is very tense.

So we would like to have a concept that measures the “spread-outness” of a random variable.
2. Variance
(1) Three Ways to Describe Spread-Outness
Basically, there are three ways for us to define the “spread-outness” of a random variable.
- Center X Method (aka. Average Deviation): Construct new random variable Y = X - 𝔼[X]. Then,

The practical meaning of the above formula is that when we minus expectation 𝔼[X] from every x, then the deviation to the right of that will by definition balanced by average, and the means of the newly created random variable has an expectation of 0. The problem is that the average deviation simply cancels out to zero (i.e. positives canceling negatives).
- Absolute Average Deviation Method: A simple to get rid of the canceling problem is to use an absolute value. So we construct random variable Y = |X - 𝔼[X]|. Then,

This is actually a fine concept that connected to mean absolute deviation. Note that mean absolute deviation is a common loss function in analytics. An example of the absolute average deviation is illustrated below,

The main problem of this method is that this function is non-differentiable at zero. So it is going to be a problem in regression, time series analysis, or it turns out other concepts too that it is very highly desirable that the function that we are working with, maybe loss function or else because we are going to fit the, for example, regression models to minimize the spread-outness of the residuals from that particular model. Variance is going to a good thing because we will fit parameters, so as to minimize variance. Whenever we do minimization or maximization, we are doing calculates. So when we have an absolute value sign on something, calculates may not be used because it is not differentiable at each point. So the nice thing for us to think about is a thing that ignores the positive or negative stuff and makes them all positives is absolutely the square method.
- Square Method (aka. Variance): Finally, based on our idea, we can then construct Y = (X-𝔼[X])²

The notation of variance on the random variable X could also be 𝕍(X), or σ²x, or σ².
(2) Variance for Discrete X: An Example
Suppose that X is a random variable such that,

Solution:

(3) The Definition of Standard Deviation
The units of the variance of random variable X are the original units of X, squared. Consequently, we will define the standard deviation of random variable X as the square root of the variance of X. For example,

(4) Famous Short Cut Formula for Variance
The function 𝔼 and the function Var on the random variable X has the relationship as,

Therefore, we have, by Fact #3

(5) n-th Moment and n-th Absolute Moment
In general, we denote the n-th moment of the random variable X as,

Whereas, we call the n-th absolute moment of the random variable X as,

(6) The Definition of Variance for Continuous X
If X is a continuous random variable, then the result of the expectation of this X is defined by,

Similarly, the variance is defined by,

(7) Properties of Variance: Claim #1
For some of c ∈ℝ,

Proof:
⇐ Suppose that X is a random variable such that ℙ(X = c) = 1
then, we have,

so that,

⇒ Assume that Var(X) = 0, without loss of generality, we can assume that X is a discrete random variable.

then,

then, A has just one member,

then,

then,

(8) Properties of Variance: Claim #2
For ∀ a, b ∈ ℝ,

Proof:
For illustrative purposes, let X be a continuous random variable,

then,

then,

then,

(9) Properties of Variance: Claim #3
For ∀ a, b ∈ ℝ,

Proof:

by claim #2,

then,

then,

So that we can have the conclusion that the variance ignores translation and the scalar multiplication has a quadratic impact.
3. Different Types of Distributions
(1) The Definition of the Moment
The moment is a series of quantitative measures that give information related to a function. If the function is a probability distribution, and X is the random variable of this distribution, the general expression of an n-th moment is defined as,

- Zeroth Moment: the total probability, and by Kolmogorov Axiom #2, this should be 1.

- First Moment: the expectation
- Second Central Moment: the variance, i.e. the spread-out
- Third Standardized Moment: the skewness, i.e. the direction of the tail

- Forth Standardized Moment: the kurtosis, i.e. how fat the tails are

(2) Bernoulli Distribution
Recall that if X follows the Bernoulli distribution, X is noted as X ~ Ber(p).

- Variance
So what is the variance of the random variable in Bernoulli distribution? The conclusion is as follows,

Proof:

then,

- Moment
The conclusion is that every moment of a Bernoulli random variable is equal to p.
Proof:

(3) Exponential Distribution
Recall that PDF of the exponential distribution is,

And X is noted as X ~ Exp(λ).
- Expectation
The expectation of random variable X that follows the exponential distribution is,

Proof:

then,

because we have,

so that we have,

- Variance
The variance of random variable X that follows the exponential distribution is,

Proof:
Because we have,

then, we have,

then,
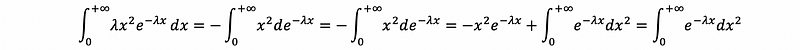
then,

as we have proved that,

then,
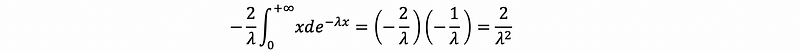
thus,

we also have,

As a result, we have,

therefore,

- Second Moment
Based on the previous proof, we can then have the second moment of the random variable X as,

- Third moment
We have the third moment of the random variable X as follows when X ~ Exp(λ),

Proof:

then,

then,

because we already proved that,

then,

- n-th moment
We can give the result of the n-th moment based on the previous proof as,

(4) Binomial Distribution
A binomial random variable X is a random variable with PMF as,

and we will denote it by X ~ Bin(n, p), where the coefficient n means the number of trials and p means the success probability. We also note that n choose x (i.e. (n x) as it is shown in the PMF above) and this is also the number of district subsets of size x from a greater set of size n. We can calculate this by formula,

where the notation “!” means factorial and it is defined by,

A binomial random variable is just the sum of independent Bernoulli trials, i.e., if Y ~ Bin(n, p), then,

where Xi ~ Ber(p) and the Xi are independent. And this is a common definition of the Bernoulli distribution.
- Expectation
For X~ Bin(n, p), we could have the expectation as,

Proof:
Suppose that we have Y ~ Bin(n, p), then,

where Xi ~ Ber(p) and the Xi are independent, then

- Variance
For X~ Bin(n, p), we could have the variance as,

Proof:
Suppose that we have Y ~ Bin(n, p), then,

where Xi ~ Ber(p) and the Xi are independent, then

(5) Geometric Distribution
A random variable X is called geometric, and we denote it by X ~ Geo(p) if its PMF p(x) is,

This random variable represents the number of coin-flips you need to see the first head, using a (possibly unfair) coin.
- Expectation
The conclusion here is pretty directly and common sense. But it could be proved based on the infinity series. However, we are not going to prove this here.

(6) Hypergeometric Distribution
We say that X is a hypergeometric random variable if,

Where x, n, D, N satisfy, D ≤ N, x ≤ n, n ≤ D, and we can denote this case by X ~ Hypergeo(n, D, N).
(7) Hypergeometric Distribution: An Example
Question: Suppose we have 34 girls and 66 boys in a class, and we want to randomly conduct a survey based on 10 students in this class. What is the probability that the survey sample has exactly 8 girls?
Solution:
In this case, D = 34, x = 8, N-D =66, n-x = 2, N = 100, n = 10, so that we have,

(8) Continuous Distribution Reminder
- Uniform Distribution: over [a, b]
- Exponential Distribution: with intensity parameter λ
- Normal Distribution: with mean μ and variance σ²