Probability and Statistics 9 | Hypothesis Testing, Type I Error, Type II Error
Probability and Statistics 9 | Hypothesis Testing, Type I Error, Type II Error
- Hypothesis Testing
(1) The Two-Sample Context De Moivre-La Place Theorem
If we can say that,
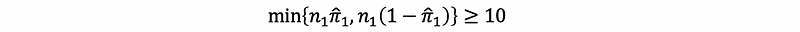
and,
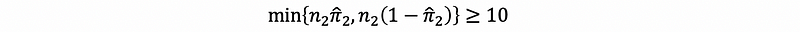
then given,
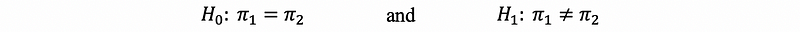
then, if we define the pooled sample proportion as,
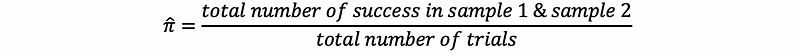
we have De Moivre -La Place theorem in the two-sample context as,
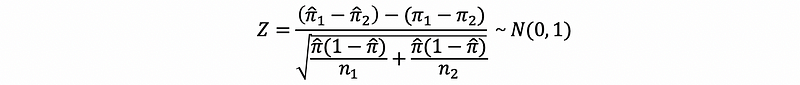
It will be wrong if we use,
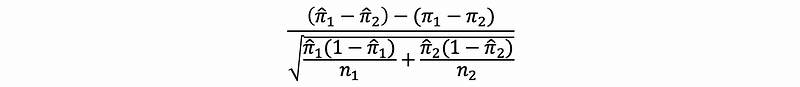
because this can be used for calculating the confidence interval but not for the hypothesis test. This is because the two samples, in this case, are exactly drawn from the same random variable. So we have to pull them together to create a single π-cap.
(2) The Two-Sample Context De Moivre -La Place Theorem: An Example
For example, some students all run a marathon (literally). They are not really designed to run marathons but we want to see if there is any difference between men and women with respect to completion rates.
Suppose we have 52 men and 40 women, and the number of successes in men is 10 with the number of successes in women is 15.
So our hypothesis should be,
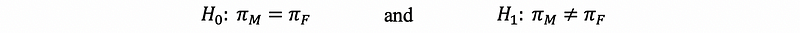
To check in both groups, the sample successes and the sample failures are ≥ 10, so it can be treated to obey the De Moivre -La Place theorem. Note that,
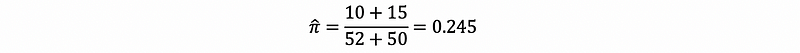
Assumes that if we have H₀ holds, then,
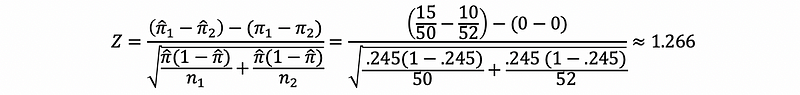
This is also to say that,
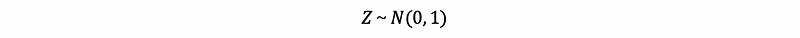
if the null hypothesis H₀ is true.
So then basically we have two ways to test this hypothesis H₀: to use a P-value approach or to use a critical value approach.
(3) The P-Value Approach
Here in order to check the null hypothesis H₀, e can plot the following graph of the standardized normal distribution as,
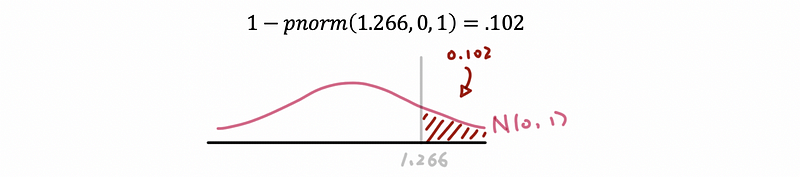
Because 2 times .102 = .204 > .05 = α, then we can conclude that there is not enough evidence at this time to reject H₀. For example, there’s not enough evidence right now to suggest different marathon completion rates.
(4) The Critical Value Approach
Here in order to check the null hypothesis H₀, e can plot the following graph of the standardized normal distribution as,
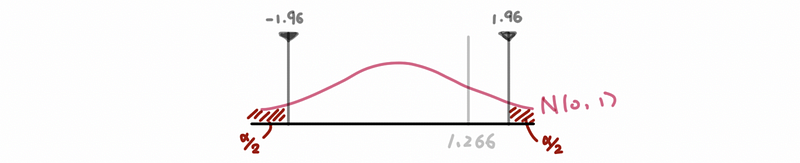
Because -1.96 < 1.266 = Z < 1.96, we do not have enough evidence at this time to reject H₀.
(5) Confidence Interval for Two Samples
Now as we have just discussed, the endpoints of the 100(1-α)% confidence interval for the difference of two proportions is therefore given by,
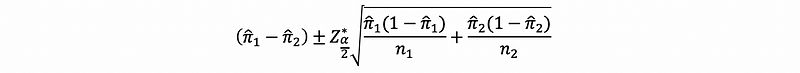
2. Fisher Transformation for Correlation Inference
(1) Hypothesis Testing for |ρ₀| < 0.50
Suppose that you have a bivariate sample {(X1, Y1), …, (Xn, Yn)} and you estimate the true population correlation coefficient ρ by way of the usual sample correlation coefficient ρ. Under the null hypothesis of
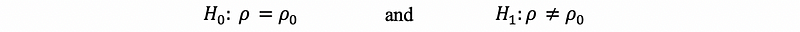
we postulate some value ρ₀ for the true population correlation between the random variables X and Y. If the random variables X and Y be jointly normally distributed and ρ₀ be equal to zero, then based on the result of Fisher,
- if |ρ₀| < 0.50, then
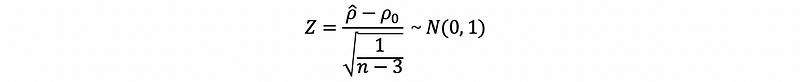
However, we can hardly find any case that the random variables X and Y be jointly normally distributed and ρ₀ be equal to zero, this is a very strong statement and it rarely happens in practice. But experience has shown that if ρ₀ does not wander too far away from zero, and if the random variables X and Y do not deviate horribly from the underlying assumption of joint normality, the test statistic has a distribution that is approximately standard normal.
(2) Hypothesis Testing for |ρ₀| > 0.50
When |ρ₀| moves closer to 1, we can no longer expect Z. This is because the Gaussian distribution with a correlation of 0.99, the sampling distribution of ρ will be severely skewed to the left and the results are no longer held. So Fisher identified the problem and then design a transform that is named after him. The Fisher transformation is,
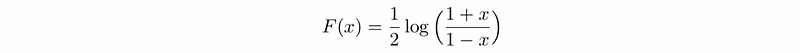
Based on that
- if |ρ₀| > 0.50, then
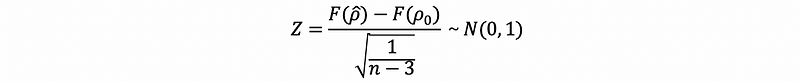
And actually, Fisher determined that F(ρ-cap) was closer to normal than just ρ-cap, but if we have |ρ-cap|<0.5, then the F(ρ-cap) ≈ ρ-cap and so the transformation is less necessary when |ρ-cap|<0.5.
(3) Confidence Interval for Correlation Inference
Suppose that,
- if |ρ-cap| < 0.50, then
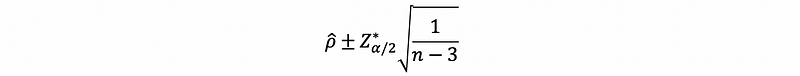
- if |ρ-cap| > 0.50, then the non-transformed confidence interval is,
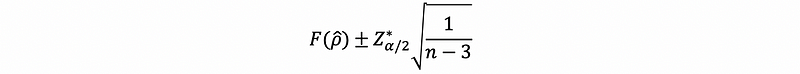
Because this interval resides in a space that doesn’t correspond to the normal space in which we expect to see or interpret confidence intervals. Given the inverse function of the Fisher transformation as,
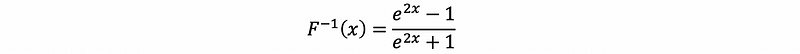
Suppose if we call the left-hand endpoint of this interval a and call the right-hand endpoint of this interval b. Then the Fisher-transformed confidence interval for ρ is given by,
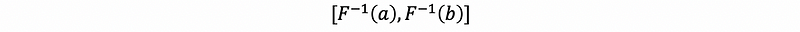
(4) Two-Sample Inference for Correlation Coefficients
Suppose we have,
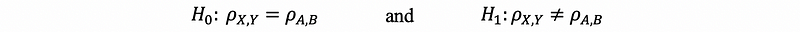
Then the appropriate test statistic is,
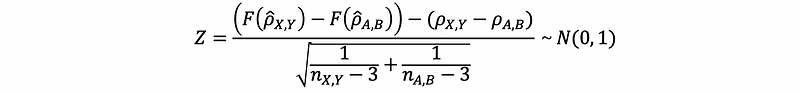
(5) Two-Sample Confidence Interval for Correlation Coefficients
The 100(1-α)% confidence interval for the difference between the two samples is,
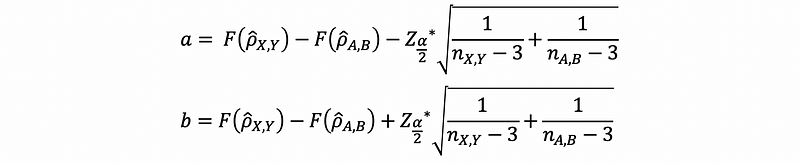
actually, we have the 100(1-α)% confidence interval as,
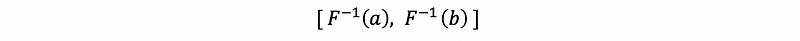
3. Two-Sample Testing For Means
(1) Case 1: If Two Samples Have the Same True Variance
When,
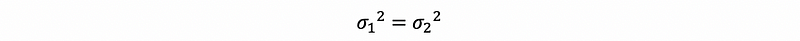
then we have hypotheses as,

Then the pooled variance is,
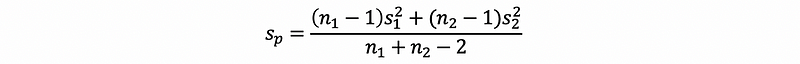
Then, the T statistics is,
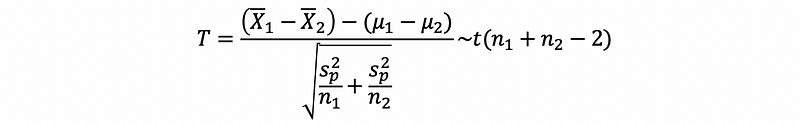
(2) Case 2: If Two Samples Have different True Variance
When,
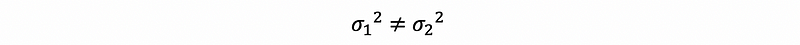
then we have hypotheses as,

Then the Satterthwaite’s degree of freedom is,
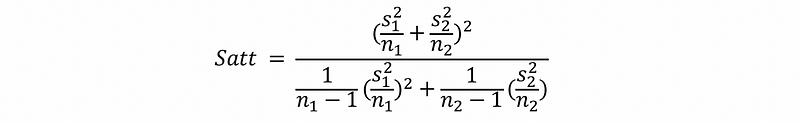
Then, the T statistics is,
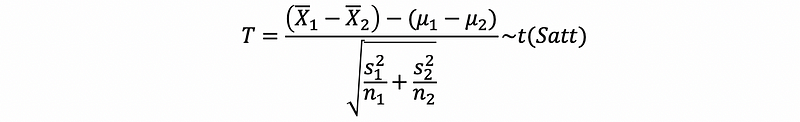
(3) Quick Checks on the Same True Variance
- Lazy Approach: Always assume that nothing is equal, we can use case 2
- Normal Approach: Use a formal statistical test to check the null hypothesis,
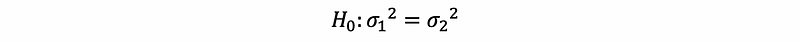
- Dirty Approach: Use F test for two sample variance …
(4) F Testing for Variances of Two Samples
If we have,
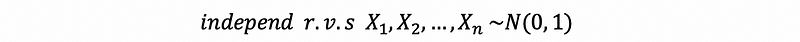
Then, suppose
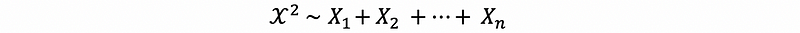
this χ² is a chi-squared random variable with n degrees of freedom.
Suppose we have X ~ χ²(n) and Y ~ χ²(m), and X and Y are independent random variables, then,
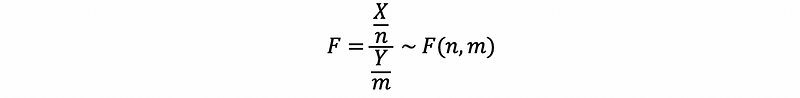
So if we have,
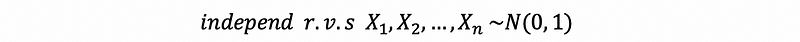
and,
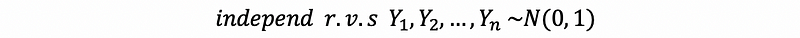
we also know that,

then,
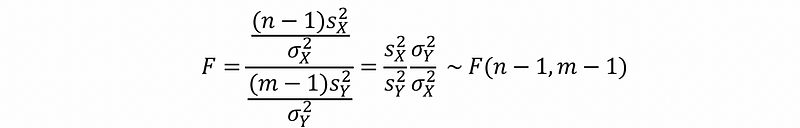
because our null hypothesis is,
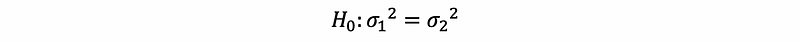
then,
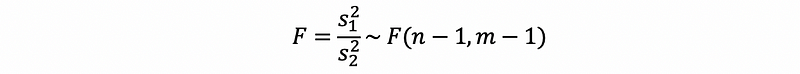
(5) Confidence Interval of the Variances Ratio between Two Samples
Based on our previous discussion, we have the 100(1-α)% confidence interval of the variance ratio as,
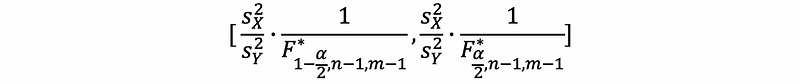
4. A Quick Review of Errors
(1) The Definition of the Type I Error
A type I error occurs when we reject the null hypothesis when it is actually true. α is the value of the highest risk of a type I error that we can tolerate.
(2) The Definition of the Type II Error
A type II error occurs when we do not reject the null hypothesis when it is actually false. β is the value of the highest risk of a type II error that we can tolerate.
(3) The Definition of the P-Value
The P-value is actually the risk of a type I error calculated through the statistics. When P-value is smaller then α, that means we can tolerate the risk of rejecting the null hypothesis when it is actually true, so we can reject the null hypothesis. When P-value is greater then α, that means we can not tolerate the risk of rejecting the null hypothesis when it is actually true, so we can not have enough evidence to reject the null hypothesis.
(4) The Definition of Power
The power of a statistical test is the probability that you reject the null hypothesis when the null hypothesis is actually false. There are three ways to increase the power of a hypothesis test: a) increase α; b) increase |μ0-μ1|, i.e. the effect size; c) Increase n, the sample size.