Probability and Statistics 11 | Correlation, Covariance, Statistical Independence, and Bivariance…

Probability and Statistics 11 | Correlation, Covariance, Statistical Independence, and Bivariance Normality

1. Correlation, Covariance, and Independence

(1) The Definition of Covariance

If X and Y are random variables, then the covariance of X and Y is defined as,

(2) A Second Definition the Covariance (aka. Product-Moment or Product-Expectation)

By definition,

then,

then,

then,

thus,

This is the second definition we have about the covariance.

(3) A Fact about the Covariance

Suppose we have two random variables X and Y satisfy,

then,

Note that we can only have this fact but NOT vice versa.

Proof:

then,

then,

then,

then,

then,

thus,

A counterexample for the invalid vice versa that,

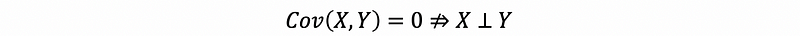
is when X and Y are jointly Gaussian, and the proof is as follows. Suppose we let X ~ N(0, 1) and Y = X². Then,

also,

then,

then,

But this does not imply that

Because Y depends explicitly upon X.

(4) The Meaning of the Covariance: Independence vs. Statistical Independence

• Independence

Theoretically, when we mean two random variables X and Y are independent, that means the joint density of these two variables is factorizable and it is defined on a rectangle-like support set. Recall:

• Statistical Independence

Empirically, when we mean two random variables X and Y are statistically independent, that means the covariance of these two variables is zero or there correlation is zero.

(5) Problems Related to the Covariance

There are basically two problems related to the covariance.

• Not invariant with respect to scalings.

Proof:

Suppose that X and Y are random variables and define that,

then,

Aside, if we have,

then,

so adding a constant to the random variable will not impact the covariance.

• You can get weird product units by covariance

Because the covariance is defined by,

so it is quite meaning less if we have this kind of units of products. To deal with this problem, we can normalize the two random variables so as to make the unit of their product equal to 1.

(6) The Definition of the Correlation

Suppose we have two random variables X and Y, if we standardize the random variables X and Y by,

if we define the correlation of X and Y as the covariance of Zx, Zy, then,

then,

Thus, we can conclude that the correlation is a normalized covariance.

(7) Properties of Covariance

• Property #1

• Property #2

• Property #3

• Property #4

• Property #5

(8) Properties of Correlation

• Property #1

where,

• Property #2

warning,

• Property #3

• Property #4

• Property #5

ρ measures only the linear dependence between X and Y. If the dependence is non-linear, then ρ is an inapplicable or inappropriate measure of dependence.

2. Bivariance Normality

(1) The Definition of Bivariance Normality

Let f(x, y) be a joint PDF of continuous random variable X and Y. We can say that X and Y are bivariate normal if the following four conditions hold.

• The marginals must be normal

• Errors for the regressior are normally distributed

The conditional distribution of Y|X=x is also normal for x∈( -∞, ∞). That is, Y|X=x is a random variable that is normal for every X = x.

• Linearity

The conditional expectation of Y|X=x, for example,

is a linear function of x; that is,

for some a and some b.

• Homoscedasticity

The conditional variance of Y, given X = x, is constant. We will denote it by,

Because it is a constant. It is independent in the functional sense of x.

(2) The Form of the Bivariance Normality

The joint density of continuous random variable X and Y is in the form of,

where, Q(x, y) is the quadratic form associate to a bivariate normal,

where,

(3) Conditional Density of Bivariance Normality

The conditional density of Y given X = x is supposed to be,

then,

then,

then,

This is a Gaussian density in slight disguise.

(4) The Mean and Variance of the Conditional Gaussian Density

• Mean

• Variance