Probability and Statistics 12 | Tower Property, Multivariate Gaussian Random Vector, and the…
Probability and Statistics 12 | Tower Property, Multivariate Gaussian Random Vector, and the Asymptotic Distribution of an MLE
- Tower Property (aka. Law of Total Expectation)
A fair coin is tossed until two tails occur successively. Let N be the total number of tosses required to terminate the experiment, then compute 𝔼[N]. Then, the essence of the tower property is the following:
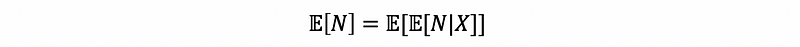
Obviously, X must be wisely chosen to be helpful, which means X should be an indicator random variable or dummy random variable. For example, we let X = 1 if the first toss results in tails and X = 0 if the first toss results in heads, then,
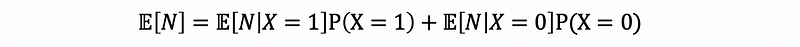
then,
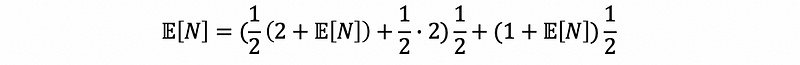
then,
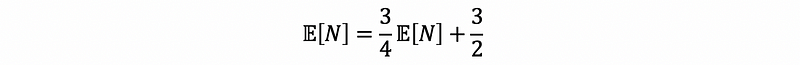
then,
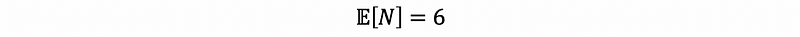
2. Multivariate Gaussian Random Vector
(1) The Definition of the Multivariate Gaussian Random Vector
If x ~N(μ, Σ), then we say that x is a multivariate Gaussian Random Vector with mean vector μ and variance-covariance matrix Σ. Suppose if x is k-dimensional, then μ∈ℝᵏ and Σ is a k × k matrix. The quadratic form of the matrix Σ is must be semi-definite, which means, ∀ x ∈ℝᵏ, then,
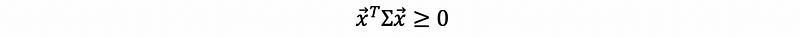
The semi-definite also means that for all eigenvalues λi of Σ, λi ≥ 0.
(2) Mahalanobis Distance
Suppose we have two vectors x and y, and Σ is the variance-covariance matrix of some underlying set of data.
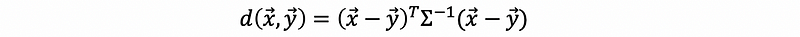
Then this distance is called the Mahalanobis distance. This distance has a key role in discriminant analysis and in the k-means clustering.
(3) Density Function for Multivariate Gaussian Random Vector
The density function for vector x is,
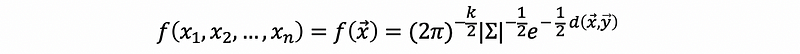
(4) Facts about Multivariate Gaussian Random Vector
Suppose that x = (x1, x2, …, xk) with x ~N(μ, Σ), then
- Every linear combination of components of x is again Gaussian. In other words,
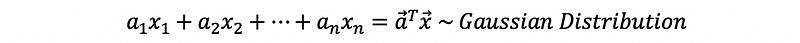
We can also have the expectation as,

and the variance as,

- For any such x, there exists a matrix A so that,
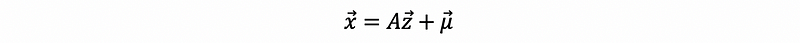
where z is a k-dimensional vector of independent standard normal random variables. In fact, A is related to a square root of Σ, which Σ always has because (a) Σ is semi-definite and (b) Σ is symmetric.
- For any k, the level curves (or level sets ) of the density f(x) are ellipsoids.
- If Xi and Xj are such that ρ(Xi, Xj) = 0, then Xi and Xj are independent.
- Two random variables that are normally distributed are not necessarily multivariate Gaussian.
(5) Multivariate Gaussian Random Vector: An Example
Suppose we have a random variable X ~ N(0, 1). Then if we define Y as Y = X if |X| > c and Y = -X if |X| < c. Then it is clearly that Y ~ N(0, 1). Unfortunately, (X, Y) is nor bivariate normal because when |X| > c, Corr(X, Y) = 1, and when |X| > c, Corr(X, Y) = -1. Whereas a multivariate Gaussian has the same covariance, or same correlations throughout the support set of the dennsity.
3. Asymptotic Distribution of an MLE
Suppose that X1, X2, …, Xn is a random sample from some density f(x; θ). Let θ-cap be an MLE vector for θ. Under a set of conditions mentioned on the homework,
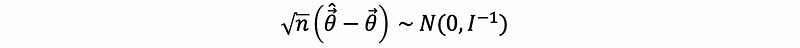
where I is the fisher transformation.
In the case when θ = θ is one-dimensional,
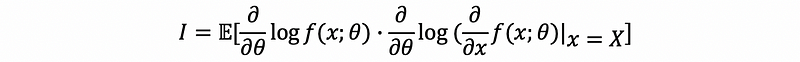
Whenever you are estimating a k-dimensional parameter vector θ that vector of MLEs θ-cap is asymptotic multivariate Gaussian.