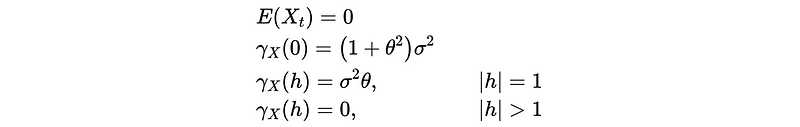Time Series Analysis 2 | Stationary Time Series and Theoretical Autocorrelation Function

Time Series Analysis 2 | Stationary Time Series and Theoretical Autocorrelation Function

1. Stationary Time Series (Weak)

(1) Problems for the Basic EDA

MA soothing and classical decomposition are just averaging the data instead of modeling. Therefore, although they can have pretty inspired graphs, they are not really a good model that provides good forecasting.

(2) The Approach of Modeling Time Series Data by ARIMA

The statistical modeling of time series data mostly focuses on modeling the first and second moments, including the most famous family of ARIMA models.

• De-trending original time series for stationary residuals: focus on eliminating the trend and seasonality in the data
• Modeling stationary residuals: we have to generate a model under the assumption that the remaining residual R_t is stationary, which is a property that we will talk about later. This R_t under the stationary assumption is also called the stationary residuals.
• Forecasting based on the stationary residuals
• Add trend and seasonality to estimate the original time series

So in this process, the critical part is when we model the stationary residuals and forecast based on them. Next up, we would like to talk about how to use the ARMA (i.e. Autoregressive Moving Average) model for modeling a stationary time series.

(3) The Definition of Weakly Stationary Time Series

The time series {X_t} is (weakly) stationary if,

• 𝔼(X_t) is independent of time t: this means the mean of the series should not change significantly over the time
• Var(X_t) is independent of time t: this means the variance of the series should not change significantly over the time
• For each h, Cov(X_(t+h), X_t) is independent of time t: this means the covariance within the same window k (aka. seasonal lag) should not change over time

Although the first two conditions seem reasonable and fair to us, the third one doesn’t seem familiar. So now, let’s introduce the next important term in the time series theory called autocorrelation.

2. Theoretical Autocorrelation Function

(1) The Definition of Autocovariance Function (ACVF)

Based on the definition of covariance, the autocovariance function (ACVF) of a stationary time series {X_t} at lag h (i.e. the distance between two observations) is,

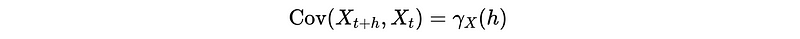
This is because that for each h, Cov(X_(t+h), X_t) is independent of time t.

(2) The Definition of Autocorrelation Function (ACF)

Based on the definition of correlation and covariance, the autocorrelation function (ACF) ρ_X(h) of a stationary time series {X_t} at lag h is then defined as,

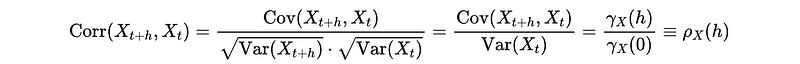
Again, you should think about proving it with Var(X_t) is independent of time t.

(3) Theoretical Vs. Computational

In time series analysis, it’s often useful to understand the theoretical/population case (e.g. we have some data distribution and we have to develop a model) and the computational/sample case (e.g. we assume to have the theoretical model and see if the data fits). Theoretical cases would help understand how the model is developed and the sample case help understands the algorithm and difference from the theoretical case.

So if we are given the theoretical distribution or time distribution of time series {X_t} and we have to prove it using the definition of stationary. This is mainly for the purpose of developing the models. If you are given data without knowing the true model, we should do some tests to find out if it is stationary. This is mainly for the purpose of choosing a developed model.

(4) Theoretical/Population Example: White Noise

So for a given model, we can prove if this model can be used to model a stationary time series.

Suppose we have a time series that follows the distribution of white noise, can we confirm that this series is stationary? The answer is yes, and we can prove it through the definition of white noise and stationary.

(4) First-order Autoregression AR(1) Process

Let’s see more theoretical/population models,

Suppose the AR(1) process follows the pattern below,

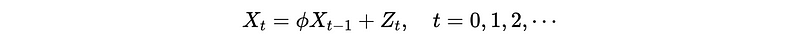
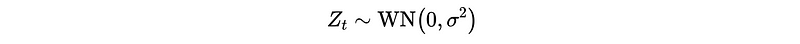
So the problem is that is AR(1) stationary?

• Prove expectation: the expectation depends on the coefficient ϕ.

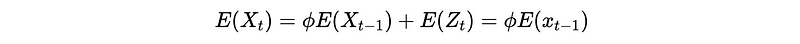
So ϕ should be 1, or 𝔼(X_t) should be 0 for the first condition.

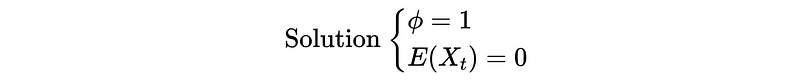
• Prove variance: We have,

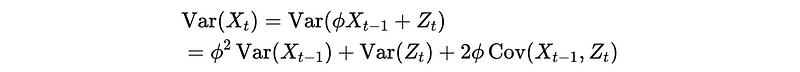
To continue the proof, we have to add an assumption of X_t is uncorrelated to Z_t for model simplification.

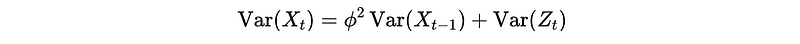
Based on this result, we can know that ϕ should not be 1 because σ² > 0.

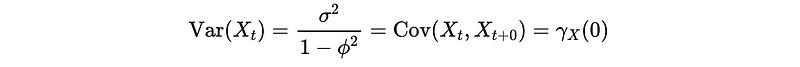
Therefore, because ϕ should not be 1, 𝔼(X_t) must be 0 if we want to prove a stationary AR(1) series {X_t}. So,

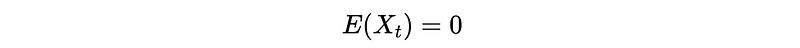
And the variance of {X_t} is,

And we can find out that it is independent of the time t.

• Prove covariance:

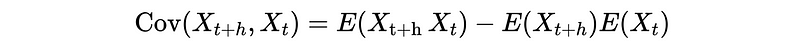
Based on our previous discussion,

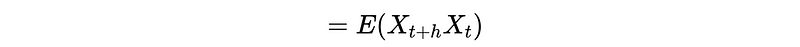
If h ≥ 1 (positive),

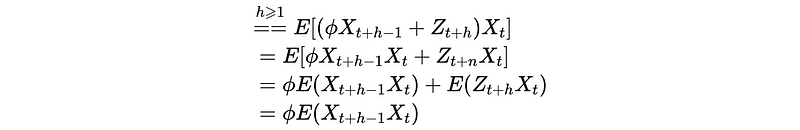
Continue this iteration, we can finally have,

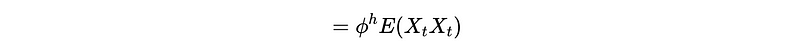
This is also,

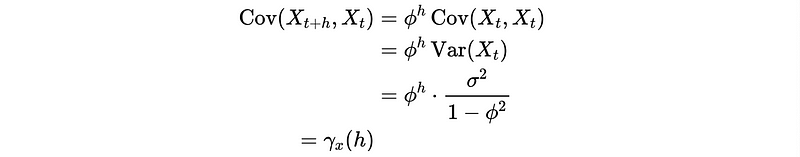
So we have proved that AR(1) can be stationary under the following conditions,

• 𝔼(X_t) = 0, |ϕ| < 1 (because the variance should be larger than 0)

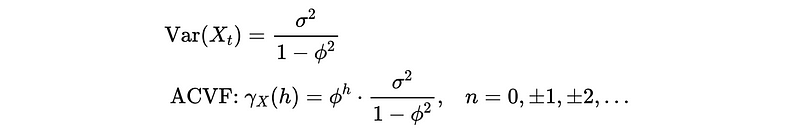
Also,

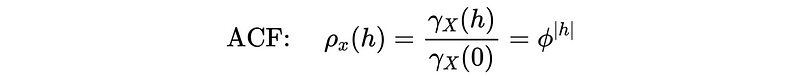
The negative case should be just the same.

(5) First-order Moving Average MA(1) Process

So now, let’s continue to talk about the MA process,

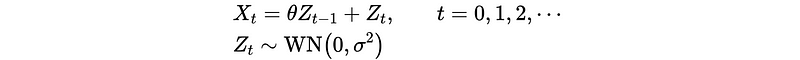
Is MA(1) stationary?

• Prove expectation:

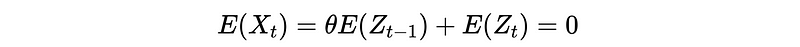
So it is independent of t.

• Prove variance:

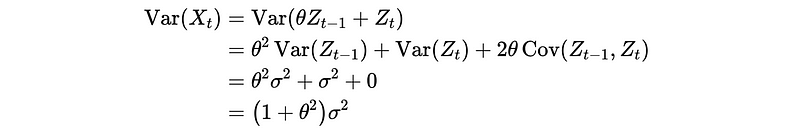
• Prove covariance:

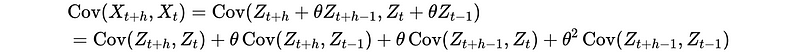
So,

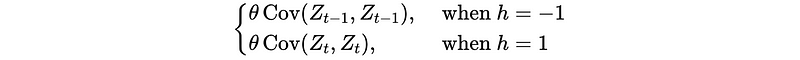
So,

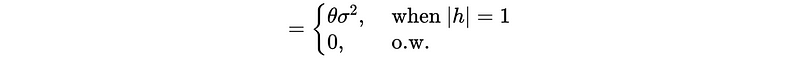
So as a conclusion, this is also independent of time t. In a summary, MA(1) is always stationary.