Time Series Analysis 4 | Stationary Condition for Autoregression Process
Time Series Analysis 4 | Stationary Condition for Autoregression Process

- Stationary Condition of AR(p)
(1) Recall: Stationary Time Series
When we talk about stationary, what we are referring to is weakly stationary. The time series is stationary if,
𝔼(X_t)is independent of time tVar(X_t)is independent of time t- For each lag h,
Cov(X_(t+h), X_t)is independent of time
Recall the following examples,
- White Noise is stationary
- AR(1) is stationary under some conditions
- MA(1) is stationary
(2) The Definition of Autoregressive Process of Order p
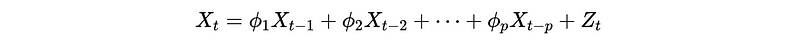
where,
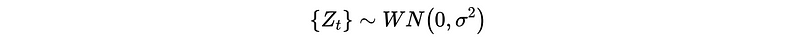
(3) Problem for AR(p)
If we want to use this AR(p) to model a stationary time series, we need to develop stationary conditions for AR(p) before the modeling process.
However, it is quite difficult to develop stationary conditions for AR(p), we would like to take a shortcut approach. The basic idea is that if we can write AR(p) as a MA(q) process, based on the fact that all the MA(q) processes are stationary, we are able to prove that this AR(p) is stationary as well. To transfer AR(p) to MA(q), one simple approach is to use a backward shift operator B.
(2) Backward Shift Operator
The backward shift operator B is a useful notational device when working with time series lags. It is defined for time series {X_t} as,
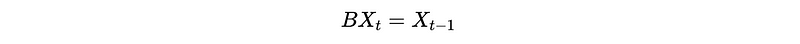
Therefore, for this time series {X_t}, we can have,
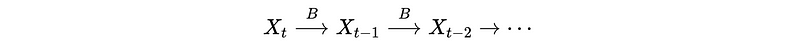
(3) AR(p) with Backward Shift Operator
Now, let’s apply this notation to the AR(p) process. For AR(p), we have
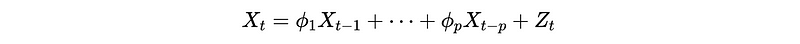
This is equivalent to,
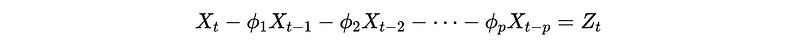
After applying B, we can rewrite the formula to,
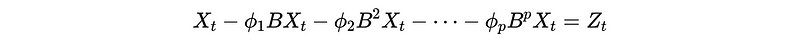
This is also,

We can denote this result to,
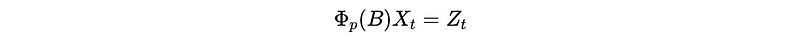
where Φ(B) is called the generating function of the AR(p) process.
(4) MA(q) with Backward Shift Operator
We can do the same thing to MA(q),
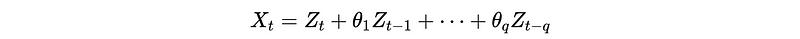
Applying B,
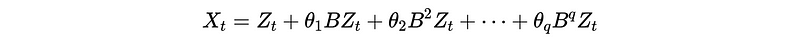
This is equivalent to,
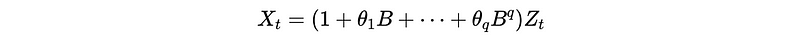
We can denote this result to,
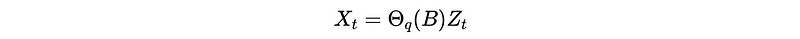
Where Θ_q(B) is called the generating function of MA(q).
(5) The Condition of Stationary AR(p)
So now it comes to our conclusion. If we can write AR(p) process as a MA(q) process, then this AR(p) process must be stationary. So for,
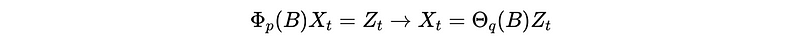
We should have,
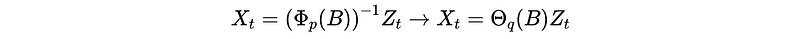
So the condition for an AR(p) process to be stationary is the inverse generating function,
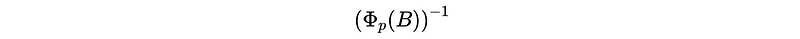
must exist.
(6) Convergent Series Expression
Now, we have the condition of stationary AR(q), but how to check if our process satisfies this condition? One conclusion is that, if we are able to write the inverse of generating function as an expression of convergent series,
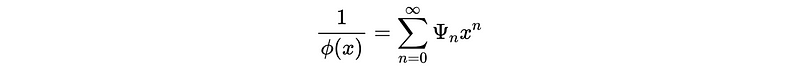
Then we can say we have an inverse function.
To have this, the roots x for,
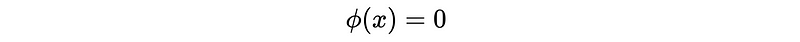
have to be outside the unit circle of,
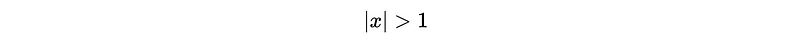
(7) Stationary AR(p) in the Forms Convergent Series
Based on our previous discussion, the AR process can be written as,
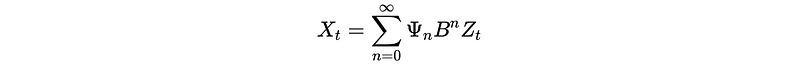
Or,
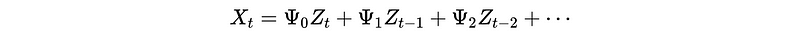
2. Examples for Stationary Condition of AR(p)
(1) Example 1
Suppose we have an AR(1) model,
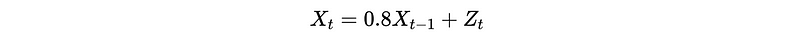
Is it a stationary process?
Solution:
- Get its generating function: by applying B
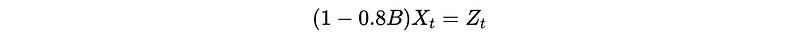
Then, the generating function is,
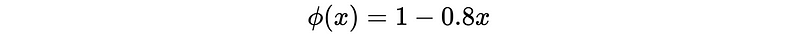
- Prove the zero roots are outside |x|< 1: Let,
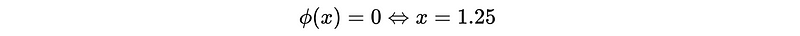
This is outside the unit circle. So {X_t} is stationary.
(2) Example 2
Suppose we have an AR(2) model,
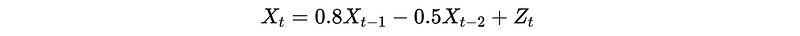
Is it a stationary process?
Solution:
- Get its generating function: by applying B
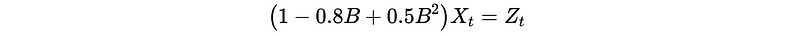
Then, the generating function is,
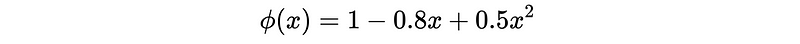
- Prove the zero roots are outside |x|< 1: The zero roots are,

Then,
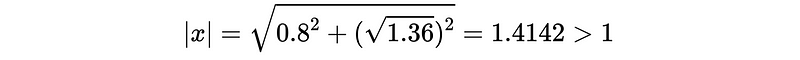
So both of the roots x’s are outside the unit cycle. So {X_t} is stationary.
3. ARMA in Python Notes
When we simulate AR or MA process in Python, we should assign the coefficients of generating function to AR_parameter or MA_parameter. Note that AR models can have negative values compared with the process expression.